1、集合与元素的定义
集合:确定的某些研究对象组成整体,用大写英文字母表示(A,B,C……)
元素:集合中的研究对象,用小写的英文字母表示(a,b,c……)
2、元素三个特性:
(1)确定性:若果集合确定,那么某一元素是否属于这个集合是确定的(属于∈或不属
于∉,即元素与集合的关系:∈和∉)
(2)互异性:一个给定的集合中,其元素是唯一的。
(3)无序性:集合中元素的位置是可以改变的。
3、集合的表示方法
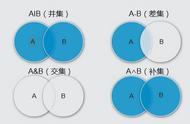
列举法、描述法(区间法)、图示法(venn图/数轴)
4、集合的分类:
空集:不含任何元素的集合,记作∅
(1)有限集:含有有限个元素的集合(∅为有限集)
(2)无限集:含有无限个元素的集合
5、常见数集
自然数集(非负整数集):N
正整数集: N*或 N
整数集 :Z
实数集 :R
有理数集 :Q
二、集合与集合1、集合间关系
(1)子集
定义:如果集合 A 的任何一个元素都是集合 B 的元素,则称集合 A 是集合 B 的子集,记作: A ⊆B(或 B ⊇ A)
集合相等:若集合A是集合B的子集,且集合B是集合A的子集,则A、B为同一集合,记作 A=B.
(2)真子集
定义:集合A是集合B的子集,且A≠B,则称A就是B的真子集,记作:A ⊊B(或B ⊋A).
总结:
[666] 若 A ⊆ B,则(1)A 、B同一集合;(2)A 是B的一部分
[666] 空集性质:∅是任意集合的子集;∅是任意非空集合的真子集
[666] 任意一个集合是其本身的子集;若A⊆B,B⊆C,则有A⊆C
2、集合间运算
(1)交集
定义:给定两个集合A,B,由所有属于A且属于B的元素组成的集合,叫做集合A与B的交集,记作A∩B(读作“A交B”).即:A∩B={x|x∈A 且 x∈B}
性质:
① A∩B=B∩A
② A∩A=A
③ A∩Ø=Ø
④(A∩B)∩C =A∩(B∩C)
⑤A∩B=A⟺ A⊆B
(2)并集
定义:给定两个集合A,B,把它们所有的元素合并在一起组成的集合,称为集合A与B的并集,记作A∪B(读作“A并B”).即:A∪B={x|x∈A 或 x∈B}
性质:
①A∪B=B∪A
② A∪A=A
③A∪Ø=A
④(A∪B)∪C =A∪(B∪C)
⑤A∪B=B⟺ A⊆B
(3)全集与补集
全集定义:一般地,若一个集合含有所研究问题涉及的所有元素,则称该集合为全集,记作U。
补集定义:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A的对于全集U的补集,简称集合A的补集,记作∁UA。即:∁UA={x|x∈U 且 x∉B}



需要文中完整截图的小伙伴可以私信我。
,