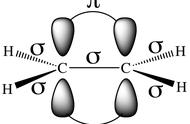
弹簧的力常数k表明键的强度,键越强力常数越大,从而振动频率也越大。从日常生活的经验我们可以知道刚性弹簧振动的基频要大于松弛弹簧振动的基频。化学键在低能振动时具有相同的性质这个公式表面化学键的伸缩振动。
同理,受到Morse 势能函数的限制,振动的能量不是连续的,而是量子化的。依旧可以使用上面的公式,其中中ω表示化学键的角振动频率,每个振动态的能量在Morse势能曲线上以横线表示。能量最低的振动(n=0) 被定义为零点能,这是一个非常重要的概念,讨论同位素效应时会用到它。把下面的公式带到Ev的表达式中就可以计算Ev。
按照键解离能的定义——“使化学键完全解离所需的能量”可知,键解离能就对应势能曲线最低处的零点能(ZPE,注意不是曲线的最低点) 与原子间距离无限大时的参考态能量之间的差值。这在上面的Morse图中已经标记了出来。
对于一系列量子化的能量状态而言,吸收光子的能量等于两个状态间的能量差,这就是光谱学中红外光谱的基础。
高能振动态的存在也被称为分子的激发振动态。对于大部分有机分子而言,其零点能之上的键伸缩振动态在常温下通常都不会明显存在。(书上这里计算了碳碳单键双键三键的例子)由于原子的振动,它们的相对位置会随着时间不断变化,这表明键长也随着时间变化。
“在特定距离上发现原子的概率”(这里不知道为什么突然问出只有一个问题)
Morse 势能函数是我们提到的第一个描述特定运动势能面的例子。化学键在Morse 势能函数定义的限制下振动。你也许会问:在某个时刻观察到一个特定的键长的概率是多少?这类似于提问在空间中特定的坐标上发现电子的概率是多少。关于这个问题的答案。
回答很简单——概率正比于波函数模的平方。

Morse 势能曲线的形状可以表示化学键的强度以及相关振动的松弛程度(即熵)。
前面大篇幅讨论了物化,这里又大篇幅讲起了量子力学,其实这里讲这些内容是为了引出下面这段话:
势阱越深,其键解离能越大,对应化学键就越强。对于类似的化学键,键越强,振动频率就越高,它表示的势能面就越狭窄(Morse势图A) 。狭窄的势阱对应于刚性振动。当化学键强度减弱时, Morse 势阱变浅,势阱的宽度增大。当振动频率变小时,该振动可以看作是松弛振动(Morse势图B 和C) 。在前面曾经提到刚性振动和松弛振动的概念对于化合物以及化学反应的情很重要。
红外光谱
以上理论的算出来的就是红外的振动峰,其实键角的弯曲、分子的摇摆和剪切振动也都是量子化的,都在红外光谱中可以观测到,但涉及对称性操作,在这里不展开了,只需了解所有的振动自由度都是量子化的(键角可以振动的范围是有限制的),每一种运动都可以通过一个势能面来描述它是刚性的还是松弛的,从而可以得出各种振动的熵的相对大小。(本章放下面这个图完全是在吓人,本章讲不到这么深。)

对于任何一个分子,其总能量表示断裂分子内所有的化学键,把分子打碎为离散的原子并移除这些原子上所有的电子所需的能量。这个值没什么意义,当然从头算可以算出来。
燃烧热是指物质与氧气进行完全燃烧反应时放出的热量。
生成热是由各种元素的最稳定单质生某纯物质产生的热效应。
要注意“完全燃烧”“最稳定单质”“反应条件”等问题。
碳氢化合物的生成热、燃烧热可以定义如下: