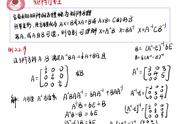先回到前面讲过的内容。在“一阶谓词逻辑”一节,命题的联接计算基于真值表,真值表应用了“=”符号,如1∨0=1。命题的推理与证明演算应用的是重言式,重言式是以蕴涵符号“⇒”或等价符号“⇔”来连接的表达式。在“算术”一节,我们讲到算术的加法计算基于特定进制下的加法表、进位规则以及一般的运算律,其中加法表与运算律都是以“=”符号连接的表达式,进位规则可看作是加法表与运算律的递归运用。本书把命题逻辑里的“⇒”与“⇔”符号与“=”符号归为同一类符号,统称为等价类符号。
“=”符号最初是用二段等长的平行线段表示“=”符号二边的内容相等。引入术语“等价类符号”,是说此类符号可以构成一个系列,且这类符号意义上都有等价类符号二边的内容或部分内容在一定意义下等价的意思。系列里的每一符号或在等价关系的性质,或等价关系成立的条件,或者其他的方面会与其他等价类符号有所不同。比如说,一些等价类符号是左右两边内容相互等价,另一些等价类符号只是某一边可以等价于另一边,反过来则不成立;一些等价类符号表示的等价关系无条件地成立,另一些等价类符号会同时带有条件,只有条件满足时,所表示的等价关系才成立。
包含等价类符号的表达式称为等价关系。本书的一个结论是:我们的认知就是确定领域内及更一般的等价关系。这一结论可分二个层次来理解,第一层是狭义的,我们所建立的各类型计算,其计算规则是用等价关系来表示,这些计算规则是相应逻辑、数学分支的核心内容。第二层是广义的,我们的知识都是应用等价关系来表示,不限于所面向的内容。对于狭义的理解,我们可以容易进行搜索来发现反例。对于广义的理解,就很难进行穷举,也不能给出一个证明,也不一定会存在一个证明的形式,本书只能在有限归纳的基础上进行简单的论述。广义的理解目前可作为假设看待。
我们试着从定义与命题二方面来论述。在数学里,我们这样定义速度:V=S/T,等号的使用是标准的。对于自然语言的使用,定义一般认为是指明被定义项的类属与种差。比如:飞机是能在空中飞行的交通工具。此定义更现代的表示是:飞机=(能在空中飞行)∧(交通工具),这样定义成了以“=”符号连接的表达,“=”符号用于建立起被定义项与其它概念间的关系。可以看出,自然语言里的“是”起到了等价类符号作用,陈述句往往可以转换为由“是”表达的句型。是否所有的陈述句都可表示为由等价类符号“是”表示的陈述句型?这里也给不出证明。
不同数学分支里的数学公式表示不同性质的内容,所建立的表达式,或称为方程,或称为函数,或是其他的名称,普遍的特征是表达式都由计算符号、计算对象符号,“=”符号连接,数学上的等价关系会随着它的投射应用带到各实证科学中。当然也存在由不等号连接的不等式,在本书的意义上,“<”“>”“<=”“>=”甚至“≠”看作与“⇒”“⇔”“=”符号同性质的系列,具体的解释我们放在下一节。自然语言使用上的灵活性,其中的等价关系并不是显而易见,但那些并不明显表现出等价关系的语句往往可以等价于明显呈现等价关系的语句或公式。比如“狮子爱吃疣猪”这一句子,很难看出其中的等价关系,;同样的意思转换句子为“疣猪是狮子喜欢的食物”,其中的等价关系就变得明显。万有引力的文字表述很难看出其中的等价关系,换成公式的表示:F=(Gm1m2)/r²,其中的等价关系就很明显。命题的意义是做出判定或断言,从而命题才具有真值。等价类符号就是命题的断言方式与标识。只是我们不一定能自觉去明确地这样使用,特别是在自然语言。
欧几里德的《几何原本》设了5条公理与5条公设,5条公设是其几何的初始,也是人们经常讨论的。5条公理较少讨论到,它们是5条关于相等关系的命题。在欧几里德的体系里,这些公理用于其几何领域的推导,也可用于其他领域内容的推导。它们具有最高的普适性(参阅2.1节)。到了近现代,各个科学领域的重大突破,主要表现为这些领域所遵循的基本等价关系的发现,比如:提到牛顿,我们想到的是他的三大运动定律与万有引力定律;提到麦克斯韦,想到的是他的电磁场麦克斯韦方程组;提到爱因斯坦,多数人首先想到的可能是E=mc²公式。更普通的,在符号“是”作为等价类符号的用法中,下面的三个不同陈述反映了历史上我们世界观的进步。
“地球是宇宙的中心,包括太阳在内的其他星体围绕着地球旋转”
“太阳是宇宙的中心,包括地球在内的其他星体围绕太阳旋转”
“太阳不是宇宙的中心,太阳只是太阳系的中心,太阳系的其他星体围绕太阳旋转,太阳系只是宇宙中渺小的一部分”
,