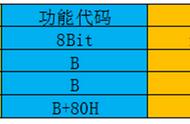
双精度浮点数相对于单精度浮点数,指数位数的增加提供了更大的指数范围,可以表示更大和更小的数值,尾数位数的增加使得双精度浮点数可以提供更高的精度,能够表示更多的有效数字位数。
双精度浮点数的表示与单精度浮点数类似,就不在赘述了。

浮点数存在的问题
上文中介绍了浮点数的表示方法,因为其此种表示方法,浮点数在实际应用中也存在了一些问题,下面介绍下浮点数常见的问题。
精度问题
我们先看一个在实际业务场景中出现的浮点数问题举例:
业务逻辑上会把用户填写的数字进行*100的操作,如果填写2.2,传入的参数就会变成220,如下图所示,传入的参数并不是预期的220,因为后端解析不了这种非整数,就会导致数据提交报错,但是如果填写的是2.5,就不会有问题。

下面来探究一下原因:
首先看一下填写的十进制数2.2 的二进制表示:10.0011001100110011001100110011001100110011001100110011...是一个无限循环的二进制小数。那么,它也就没办法表示为一个精确的浮点数,这个不精确的浮点数在进行乘法运算后,再转化为十进制,这个过程中,误差会累积变大,最终2.2乘以100得到的结果是220.00000000000003,而不是精确的220。
但是,十进制数2.5 的二进制表示为10.1,是一个正常的二进制小数,因此它可以表示为一个精确的浮点数,经过乘法运算和十进制转化,仍是精确的250,就不会出现上述问题。
这个问题就是浮点数最常见的问题之一的精度问题,根本原因是浮点数表示的精度有限,无法精确表示所有实数,某些十进制数可能无法准确表示为有限位数的浮点数。
舍入误差
前面的例子中有提到2.2的二进制表示是无限循环的,由于浮点数的尾数部分有限,转换为浮点数时就会产生舍入误差,这个也是引起上面问题的原因之一。
比较问题
由于舍入误差,浮点数的比较操作可能会产生意外的结果,在某些情况下,两个看似相等的浮点数进行比较可能得到不相等的结果。比如下面这个实际项目中的例子:
页面展示的数据计算的可开票金额=51,496.64,填写该金额后,校验不通过,系统提示“不能大于可开票金额",无法提交开票申请。

接口返回的数据如下图所示,并不是计算得出的预期结果51,496.64,因此导致前端填写的数据与此数值比较时,无法验证通过。