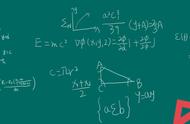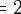有关e的指数函数在数学中应用非常广泛,如人口增长,年利率计算,放射性衰变都离不开e的身影。

指数函数e^x在几何中最重要的一点就是:曲线上任一点切线的斜率与曲线在该点的高度成比例,且为一个常数,基于这样的事实,我们可以很容易的求出指数函数曲线下的面积
下面我们以Y=e^(x/b)为例,来计算该曲线下的面积,计算曲线下的面积,我们一般很容易想到一元微积分,但这里我们抛开微积分的思想,用形象直观的几何原理来演示,

首先Y=e^(x/b) 的导数是(1/b)*e^(x/b),所以切线在X轴上的投影就是一个常数b,当切线从右往左移动到负无穷时,所经过的区域就是X轴上方的切线所扫过的区域,图中所示
因为任意点的切线在X轴上的投影始终为常数b,所有切线形成的切线簇是一个底为b,高为e^(x/b)的直角三角形,即切线簇区域的面积等于直角三角形的面积S=1/2 b*e^(x/b)
进一步显示,当切线向左平移时,切线与X轴的交点变成了一个公共点,均包含在图中斜线区域的直角三角形中,因此Y=e^(x/b)曲线和(-∞,X)区域之间的面积是直角三角形面积的两倍,它等于b*e^(x/b),这和一元微积分得到的结果是一致的。