初中几何的一些重要定理和公式在课本上不会讲到,但在各类考试中还是有可能会出现。下面通过一道题学习这两个重要的知识点:海伦公式和三角形内角平分线定理。
△ABC的三边长分别是:AB=13,BC=14,AC=15,D是BC的中点,AE是∠BAC的平分线。如图所示。问△ADE的面积是多少?

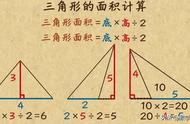
一个三角形只知道三条边的长度,计算面积需要用到海伦公式:
,
其中a、b、c是三角形的三边长,p=1/2(a b c)。
在本题中,应用海伦公式,可计算出△ABC的面积=84。
因为△AED的面积/△ABC的面积=ED/BC,所以只需要知道ED的长,即可计算△AED的面积。
这就需要用到三角形内角平分线定理:
三角形内角平分线内分对边,所得的两条线段与这个角的两边对应成比例。
以本题为例,因为AE是角平分线,所以有:。
带入数据可以解得BE=6.5。
因为D是BC的中点,所以BD=7,这样就得:ED=0.5。
所以△AED的面积=0.5÷14×84=3。
小结:海伦公式和三角形内角平分线定理虽然课本上不讲,但却是很重要的知识,考试中可能会出现,或者应用该知识能大大简化题目难度,还是很有必要掌握的。
,