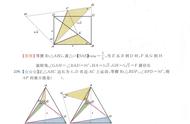
前两天讨论了一道初一的因式分解求最小值问题,这道题考量了两个知识点,如果不清楚的可以翻看前面的评论。这里要讨论的是如何用excel提供的规划求解工具来求解这类题,其实规划求解特别适合求解这类问题。

Pic.1 极值问题
首先,设定a,b,c = C3, C4, C5, 并设定初始值为0,0,0,
C2=a b c=C3 C4 C5
C6=abc ab bc ca a b c
如下图示,

Pic.2 初始设定
然后打开规划求解窗口,并设定如下
目标:$C$2, 最小值, (C2=a b c=C3 C4 C5,求其最小值)
通过可变单元格:$C$3:$C$5 (变化a, b ,c)
设定约束,$C$3:$C$5=整数
C6=abc ab bc ca a b c=2003

Pic.3 规划求解的边界条件
选择求解方法为非线性 CRG,
并点击求解,
大约半分钟不到的时间,可以得到一个合理解,如下图,

Pic.4 求解结束
并确定,得到一组合理解如下,Min(a b c)=171,

Pic.5 合理解
是不是很方便呢?
其实除了这类极值问题,它还很能解方程,大部分小学初中的问题都可以用规划求解来解决。
,