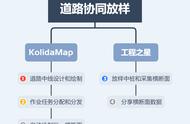
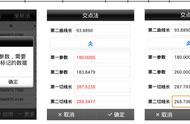
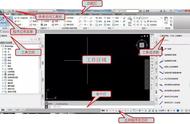
(如果您对此很熟悉,请绕道) 线 元法的出现,可以说从根本上解决了线路的计算问题。在《灵活使用交点法定义线路》中可以看到,“灵活”是相对于传统的定义方法的,对于定义任意线路仍然存在较大的缺陷,比如无限制的偏转角,虽然可以使用多交点方法来定义,但却因此显得更加繁琐和复杂。 01 线路定义的“一统江湖” 线元法用七个元素来定义一个线元: 1、起点里程(K) 2、起点坐标(C) 3、起始方位角(A) 4、线元长度(L) 5、起点半径(sR) 6、终点半径(eR) 7、曲线偏向(T) 如果用U(K,C,A,L,sR,eR,T)表示一个线元,则一条线路则是U的有序集合{U1,U2,...Ui}。用这七个元素可以轻松定义直线、圆曲线以及缓和曲线,当sR=eR=∞时即为直线,当sR=eR≠∞即为圆曲线,此外的情形即为缓和曲线。线元法的定义是以缓和曲线为模板,将直线和圆曲线作为两个特例从而在线路定义上“一统江湖”。 02 算法统一 使用数值积分能完美解决缓和曲线的计算问题,在《广义地理解和使用线路》(这篇文章里的切线支距需要改为法线支距,在一次培训中发现,说声抱歉)以及《线路:您也可以搞定线路正算》中介绍了统一计算模型(针对三次抛物线的计算模型,如果缓和曲线类型不同,改变算法即可)。 03 各类线路计算软件的区别 在一些仪器内置软件或PC软件中,有把线元法叫积木法的,很形象,但不准确,如果看到,就理解为线元法。 线元法的计算模型是一致的,各类软件的区别主要在于数值积分方法(有N多种,可以查阅相关书籍)的不同,从而也导致计算精度的不同,对于一般工程的缓和曲线计算,大多数软件没有问题,对于《线路计算的比较测试》中的线路,大多数软件是存在问题的。 在fx5800\fx5800p中流行的一个采用了高斯-勒让德数值积分方法的,速度快(无需迭代),适合计算器使用,但其不能计算大偏角(超过90度,计算精度降低甚至错误。当然就算是这种情况也比较少见)的缓和曲线,在应用时需要注意。如果确实要使用这种方法,可以采取将线元截断成几个线元来处理。 04 Anew对线元法的处理 (Anew没有发布也没有发布日程,使用其他线路计算软件一样,基本能满足一般工程需要。) 为了符合线元法的广义定义,Anew在定义线元法时可以允许非切向连接,即可以允许线路转折,这对于大量非常规线路(比如场地边缘)是必要的。 线元法输入数据比交点法要多很多,为了实时对照,在每输入一个线元后,Anew在线路切向连接时(需要在设置中勾选一下,默认是切向连接)会自动计算出下一个线元的起点里程、坐标、切线方位角,只需要输入下一个线元的长度、起终点半径、偏向即可。避免全部输入完成才能看到结果,对于检查错误十分不利。 没有搞明白,为什么很多的线路计算软件不支持断链的处理,从而让我们把一个项目的线路按断链点位置切成了几段来处理,有时候容易搞忘记从而导致错误。其实这个算法并不是太复杂,Anew在线元法和交点法的定义表中均有断链的部分,不管何时输入,都会对里程进行更新。对于新手,容易忽略断链,这很危险,因为建筑物会因此在线路方向上移位。

,