本文为“第二届数学文化征文比赛”参赛作品,未经授权不得转载,点击图片查看第二届数学文化征文比赛通知。
《两位数除以一位数的笔算除法》教学设计与反思
作者:吴晨璐
作品编号:019
投稿时间:2020.7.23
教学内容
二年级下册《除法竖式计算》P62-63
教学基础
100以内加减法口算及竖式计算;表内乘除法
平均分;有余数除法口算意义的理解;解决除法的多样性策略及多种表征方式
教学目标
知识性目标
理解除法竖式的算理
熟练掌握除法竖式的算法,并形成良好的答题规范
了解除法竖式的相关数学文化历史,充盈数学涵泳
掌握除法竖式模型应用的规律及运算特点
把握除法竖式余数和除数的大小关系
能够熟练运用除法竖式解决生活中的实际问题,并能对结果的实际意义做出解释
过程性目标
在经历观察,操作,交流,互动中经历探索除法计算策略的多样性
经历与他人交流各自算法的过程
在合作探究中经历操作除法竖式的形成及体验感受不断优化过程
在了解数学史知识过程中加深对除法竖式的理解
在数学文化融入教学中体验数学创作的数学精神和文化魅力拓展视野
借助名人名言等感受数学的简约美,提升数学境界。
教学重点
理解除法竖式的算理,掌握并熟练运用除法竖式的算法。
教学难点
探究理解除法竖式的形成过程
教学关键点
除法竖式的书写的认同和意义的理解
数学史引入深化对除法竖式形成过程的理解
除法竖式创造技术
摆放形式的抽象,操作程序的优化,操作程序的抽象概括
教学两层次:
①直观感知构建除法竖式模型;②解释应用模型归纳竖式运算规律
教学特色
教学中考虑采用探索发现的构架
通过数学文化的引入(数学符号和除法竖式)加深对于除法竖式形成过程的理解。
教学过程
(一)旧知回顾,激活学习经验
课前出示习题(包含:加减乘除口算,加减法竖式)
(1)口算32 30=?35 6=?(2)笔算(列出加法,减法竖式)
师:结合这些题目思考一下:口算和笔算有什么不同呢?
预设1:口算直接写出答案,笔算又要写过程又要写答案
预设2:笔算虽然麻烦,但是不容易错
情境引入:出示13个苹果
问:老师今天拿了13个苹果,想每4个苹果放一盘,这该如何解决呢?
出示算式:13÷4=?
师:怎么计算,你有好主意吗?
预设1:动手分一分(上台展示)
预设2:借助画图,列减法算式:13-4-4-4=1(师:这里的“1”是商的意思吗?)
师:你能说说你这样列式的理由吗?
生:13个苹果4个4个分这样的3次还剩1个不够分。
师:谁听懂了,谁能再次复述把话说清楚?
引导:13,4,1分别表示什么意思?(3又在哪里?)
13表示苹果总数;4表示每份4个;1表示还剩1个不够平均分;
3即式子中4的个数表示能平均分3盘
所以横式可以写成:13÷4=3(盘)…1(个),注意单位!
师:还有其他不同的想法吗?
预设3:乘法口诀,想3×4=12,13-12=1(想乘做除)
师:你是说你想4和几相乘的积接近13,而且比13小对吗
师:还有其他的吗?今天咱们就来认识一种新的办法
板书课题《两位数除以一位数的笔算算法》
(二)沟通类比建构模型
名言呈现
如果一个人能把除法做好,那么其他的运算对他来说轻而易举,因为加减乘除都包含在除法运算中。
----帕乔利(意大利数学家,1494年)
师:为什么说加减乘除都包括在除法运算中了呢?
既然竖式体现过程本节课就借竖式来验证一下吧
问:对于除法竖式你想知道什么?
预设1:除法算式又是怎么来的?
预设2:如何列除法算式?
预设3:为什么要列除法算式?
师:首先咱们解决第一个问题:怎么来的。来当一回小小数学家吧!
小组合作自主探究
思考:大数学家帕乔利的观点如何在竖式中呈现出来?
教师选取典型结果呈现于黑板

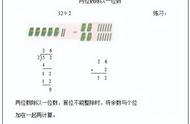
预设1:除法竖式(如图1)
师:同学们这种形式你们觉得怎么样?这是他心中的除法算式,老师有两个思考
问题①:都说笔算既要写过程又要写答案,为的是计算更准确,这里有过程吗?
问题②:帕乔利说的观点在这个算式中印证了吗?
小结:这种形式不能说错,但是也许有更好的办法。
预设2:连减的笔算形式(如图2)
师:同样思考老师的以上两个问题
生:计算体现了过程,但是不简便
生:这是减法竖式不是除法竖式,也没有把加减乘除包括在内。
小结:的确。但一点值得表扬:能类比减法推导除法横式的办法用在竖式上。
师:在创造的道路上注定会遇到各种困难。只要齐心努力相信一定可以战胜它们!
除法竖式的创造
在之前的课程中,我们学会用减法推导解释除法口算算法
思考:(1)能否借助减法竖式类比解释除法竖式呢?
(2)帕乔利的话合理性何在?
师:连减能体现过程但是不属于除法范畴
引导:减法竖式中诸如减数,被减数,减号等元素均具备,所以属于减法范畴
师:怎样变就可以转化成除法?
体现除:13÷4=3(次)…1(个)
生:将除法中的除数,被除数,除号等都加入
师:谁愿意上台尝试,其他有想法同学也可以申请上台修改
引导:减法竖式中12是被除数,如何在此基础上添加等号,除号,除数?
文化点:“÷”→“)”,“=” →“——”的修改(除号形式的纠正)
师:咱们扮演数学家的角色,自然也要进入当时的社会环境
在那个时候,除号“÷”仍未诞生,1544年德国数学家斯蒂菲尔(M.stifel)在他出版的《整数算术》中以一个或者一对括号作为除号,例如“8)24”表示“24÷8”
小结:所以我们将“÷”改写成“)”
师:除此而外,从15世纪起数学家们陆续创作了自己的数学符号,等号也包括在内。
比如阿拉伯人盖拉萨迪用“∫”表示等号,德国人缪勒(1436-1476)和意大利数学家帕乔利(?-1517)用一条长长的破折号“——”表示等号。
在经历了诸多变化之后,才最终定下了英国数学家雷科德的在“——”上加一线,即用两条平行直线表示相等的“=”。
师:同学们,帕乔利用了什么符号?(“——”作为等号)
小结:所以我们需要对“=”也做出修改为“——”形式
体现“加”
师:借助减法算理细化理解3(在等号上以3个“1”呈现)表明连续减去3次4
问:如何体现加?(三个1相加)那现在属于除法竖式了吗?
生:有过程,有结果,有乘法的所有元素了,所以属于除法竖式。
问:大数学家帕乔利的话印证了吗?
生:有减,有加,有除,但是乘在哪里?
学生思考自主探索
师:连减部分的三个4能不能改进?
预设:3个4就是3×4=12,可以将下半部分简化为12
师:不错,不仅体现乘,还把数学竖式的简约美充分展现出来了
总结:同学们真是太厉害了,除法竖式已被我们创造出了!
(三)科学性数学文化的印证力量
环节一:切实感受重走数学家的道路

师:我们借助已有经验创造出了除法竖式,那个年代的人是怎么样创造的好奇嘛?
师:其实在2000多年前古人和我们也有类似的思考
(出示中国的办法:“直除法”,如图1)
师:熟悉吗?(连减)
师:这种方法怎么样?
生:好理解,但数字大的时候麻烦,要写好几个5
师:于是1000多年后人们想出了一个类似的除法 竖式(右图2)
师:熟悉吗?
生:类似我们创造的第三步,和简化之前的除法开始类似了。
师:看来我们同学都拥有数学家的智慧!
环节二:体验数学的简洁美