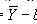全文共967字,预计阅读时间:3分钟
之前我们已经学习了关于直线的倾斜角和斜率的相关知识,为了保证学习效果,同学们要及时回顾,同学们还有哪些疑问也可以留言提出哦!
今天,我们将学习直线的方程有哪些表示方法,快看下去吧!

在之前的学习中,我们了解了“一点和确定的方向可以确定一条直线”,同时也学习了直线的斜率,那么如果我们知道一条直线的斜率,并知道其经过一个定点,是否就可以得到这条直线的方程了呢?
假设一条直线经过点(x0,y0),而且其斜率为k,那我们取这条直线上另一个不同于(x0,y0)的点(x,y),我们可以根据斜率的公式得到k=(y-y0)/(x-x0),也就是y-y0=k(x-x0)。
这种用直线上一个定点和该直线的斜率表示的直线方程式就是直线的点斜式方程,简称为点斜式。

我们知道两点确定一条直线,因此知道一条直线上的两个不同点的坐标(x1,y1)和(x2,y2),我们也可以得到直线的方程。
取直线上一个不同于(x1,y1)和(x2,y2)的点(x,y),根据直线斜率的公式得到k=(y-y1)/(x-x1)=(y-y2)/(x-x2)。
这便是直线的两点式方程,简称为两点式。

直线上有两个比较特殊的点,即为直线与x轴和y轴的交点(a,0)和(0,b),当我们知道直线的斜率k的时候,根据直线的点斜式方程我们可以得到y-0=k(x-a)和y-b=k(x-0),即y=k(x-a)和y=kx b;
根据直线的两点式方程我们可以得到k=(y-0)/(x-a)=(y-b)/(x-0),即x/a y/b=1;
我们将直线与y轴交点(0,b)的纵坐标b称为直线在y轴上的截距,因此我们又称方程y=kx b为直线的斜截式方程,简称斜截式;
我们将直线与x轴交点(a,0)的横坐标a称为直线在x轴上的截距,因此我们又称方程x/a y/b=1为直线的截距式方程,简称截距式。

通过上面几种直线方程形式,我们可以发现直线方程是一个关于x和y的二元一次方程,也就是Ax By C=0,其中A和B不同时为0,这就是直线的一般式方程,简称为一般式。

今天,我们学习了三种直线方程的形式,希望可以帮助同学们更好的进行高中数学学习哦!
同学们有任何不懂的内容可以留言提问,如果有需要的话我们会有习题类推文哦!
下一期我们将继续讨论数学学习的相关问题呀!如果你想知道更多,请关注我们哦!
本文由如意王工作室原创,欢迎关注,带你一起长知识!
,