20世纪60年代,韦恩赫·冯·布劳恩撰写了一系列关于太空飞行的文章,其中一些文章发表在《科普月刊》上。这些文章收集成书,名为《空间前沿》(第一版,霍尔特,莱因哈特和温斯顿)。这是一本非常易读的书,讲述了火箭的工作原理,以及在太空中的飞行和安全问题。在其中一篇文章中,冯·布劳恩解释了为什么卫星能够在地球轨道上保持稳定。
他在文章的开始提出,如果我们可以像下面图中那样,水平的、更快的速度抛出一个物体,会发生什么?“最终,”他写道,“向下弯曲的轨道曲率将与地球的曲率相等。”(这一说法并不完全正确,但与下面的情况相比,这只是一个微小的错误。)最重要的一点是,当子弹移动得越来越快时,就会达到远离地球轨道的速度。再加上向下的方向不断变化,因此子弹永远不会靠近地面——它位于地球轨道上。这实际上是引力平方反比定律的一个奇妙的特殊特征。如果引力不是平方反比,这种情况是不可能发生的。一般来说,轨道是椭圆的。下面的这个图片最初由艾萨克·牛顿爵士的《公理》(1687年)收录。

在这之后,冯·布劳恩又提出,当子弹以更快的速度射出时,“它的轨迹将减少偏转,因为其离心力会因更高的速度而增加,更有效地抵消了地球引力。”在这一点上物理学家很迷惑。离心力?这和卫星运动有什么关系?
接下来,冯·布劳恩绘制了一张地球轨道卫星的图片。作用在卫星上的是两种力:引力,把卫星拉向地球;离心力,把卫星推开。他写道:“当一个小质量物体通过大物体的引力场时,如果恰好有足够强的离心力平衡了大物体的引力,就会出现圆形的运转轨道。”“如果引力和离心力之间的平衡不是完美的,……小物体将遵循椭圆路径围绕大物体转动。”

牛顿会怎么说呢?他也会画出作用在卫星上的力,然后采用“力=质量×加速度”公式计算,但首先,他选择一个“惯性系”,因为他的定律只在惯性系中起作用。惯性系是指我们抛球时,球以恒定的速度(即直线恒速)离开我们。由于这种情况并不都是发生在地球上,所以牛顿选择的框架是包括地球之外的更全面的框架。这一框架近似于太阳系,太阳处于静止状态,地球相当精确地围绕着它旋转,一年旋转一圈。这样的惯性系与冯·布劳恩提出的模型相似,因为任何非惯性的东西都不能很好地与他提出的地球和卫星框架结合在一起。
在惯性系中,如果卫星真的存在两个相等但相反的力,就像冯·布劳恩画的那样,那么它的合力将为零。所以卫星不会加速,它会以恒定的速度直线运动。由于轨道卫星没有直线移动,冯·布劳恩的图片和他的解释都不可能是正确的。

什么都无法支撑月亮!
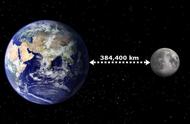
事实上,没有什么东西能支撑月亮。正如牛顿的惯性系分析中预测的那样,月球完全处于引力的压力之下。换句话说,月球会坠落,因为在这样的框架中,月球上只有一种力:引力。引力给月球一个加速度。这并不意味着它的速度必须改变,或者它必须离地球更近(尽管实际上这两件事在一个月里都会发生,但这并不是一个重要的问题)。如果牛顿的F=ma公式是在引力作用下的一般情况下求解的,则得到的运动是直线、圆、椭圆、抛物线和双曲线。在自然界和纯数学的对应关系中,这些曲线就是我们取一个锥体,并将它切成任意方向时所产生的曲线。
即使月球的轨道是圆形的,但它的运动方向也会发生变化,这是一种加速度。(加速度是速度的变化,这意味着加速度可以改变物体的速度,或者改变物体运动的方向,或者两者兼有。)月球和其他所有的卫星,在引力作用下都会像苹果一样坠落。苹果的速度改变但运动方向不变,而月亮的运动方向改变,速度没有变化。如果月球现在我们上空,那么45分钟后它会下降到地球的另一边。到那时,向下的方向完全颠倒了,月球将再次向地球另一面的人坠落,在我们第一次看到它的90分钟后返回到我们身边。当然,它永远不会撞击地球,因为它始终存在着横向运动。月球离地心引力较弱的地方远得多,因此需要整整两个星期才能落到地球的另一边。