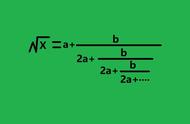大家都知道 4的平方根是2,9的平方根是3,对于非整数平方的数求平方根,通常老师会要求学生记住=1.414 =1.732,那么若遇到求其他数的平方根怎么办呢?
下面就介绍一个求任何一个数的平方根的方法:
1) 在如图所示的网格纸上写下一个数71824,从整数部分的个位开始向左每隔两位数标一个逗号,将数分成几段,表示所求平方根是几位数;
2) 先看左边起第一段7,哪个数的平方不超过且最接近7?对,是2。在7的上方写上2,在7下面一行的第F列写上2,在7下方写上2乘以2的积4,7-4得到余数3。
3) 将最上方的2乘以2,得到4,将4写到余数3下面一行的第E列。将第二段中的两个数字18下移到余数3的后面,现在看哪个数放到4后面的第F列后得到的数再乘以这个数会小于且最接近318,答案是6,也就是46x6=276。将6写到第二段数字18中8的上方,将276写到318的下方,318-276得到余数42.
4) 重复上一步,将最上方的26乘以2,得到52,将52写到余数42下面一行的第D和E列。将第三段中的两个数字24下移到余数42的后面,现在看哪个数放到52后面的第F列后得到的数再乘以这个数会小于且最接近4224,答案是8,也就是528x8=4224。将8写到第三段数字24中4的上方,将4224写到4224的下方,两数相减得到余数0。
到此,计算完成,71824的平方根是268.

若所有分段中数字均使用完后,余数不为0,则可补00,以便计算平方根的小数部分,如图下半部分的示例。若要求平方根的计算结果保留到小数点后n位,则计算到小数点后n 1位,然后对计算结果四舍五入即可。如图所示,218的平方根保留到小数点后3位是14.765。
,