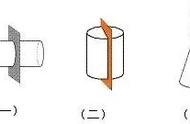
(1)认识圆柱各部分的名称:
上下两个圆面叫做底面,
圆柱的周围叫侧面,
圆柱两个底面之间的距离叫做高。
(2)圆柱的特征:
圆柱的上下底面是两个圆,它们是完全相同的;圆柱的侧面是曲面;圆柱的高有无数条,高的长度都相等。
(3)沿高剪开:圆柱的侧面展开后是长方形(当圆柱底面周长与高相等时,展开后是正方形)。

这个长方形的长就是圆柱底面的周长,宽就是圆柱的高。
2. 圆锥
(1)认识圆锥各部分的名称:

下面一个圆面叫做底面,它周围叫侧面,从圆锥的顶点到底面圆心的距离叫做高。
(2)圆锥的特征
圆锥的底面都是一个圆。圆锥的侧面是曲面。一个圆锥只有一条高。
(3)圆锥的侧面沿着一条母线展开后是一个扇
形,这个扇形的弧长等于圆锥的底面周长,半径等于圆锥的母线长。(如下图所示)
(二)、基本公式
1、圆的知识
圆的周长=直径×π=半径×2×π
C=πd =2πr
逆推公式有:
直径=圆的周长÷π
d = C÷π
半径=圆的周长÷π÷2
r = C÷π÷2
圆的面积=半径的平方×π
=(直径÷2)2×π
=(圆的周长÷π÷2)2×π
S=πr2
=(d÷2)2×π
=(C÷π÷2)2×π
2、( 1 )圆柱的侧面积:把圆柱侧面沿高展开,得到一个长方形(或正方形),长方形的长是圆柱的底面周长,长方形的宽是圆柱的高。
圆柱的侧面积=底面周长×高
=直径×π×高
=半径×2×π×高
S 侧=C h=πd h=2πr h
逆推公式有:
圆柱的高=圆柱的侧面积÷底面周长
=圆柱的侧面积÷(π×高)
=圆柱的侧面积÷(半径×2×π)
h=S 侧÷C
圆柱的底面周长=圆柱的侧面积÷高
C =S 侧÷h
(2)圆柱的表面积
=圆柱的侧面积+圆柱的底面积×2
S表=S 侧 2S底
(3) 圆柱的体积=底面积×高
V柱=S h=πr2 h
逆推公式有:
圆柱的高=圆柱的体积÷底面积
h=V柱÷S
圆柱的底面积=圆柱的体积÷高
h=V柱÷S
3 ( 1 )如果圆柱的侧面展开是一个正方形,那么这个圆柱的高和底面周长相等。
( 2 )半个圆柱的表面积= 侧面积÷2 +一个底面积+直径×高
(3)圆柱的表面积
=侧面积÷4+半个底面积+直径×高
4、圆锥的体积=底面积×高×1/3
V锥=1/3Sh
逆推公式有:
圆锥的高=圆锥的体积×3÷底面积
h=V锥×3÷S
圆锥的底面积=圆锥的体积×3÷高
S= V锥×3 ÷h
5、等底等高情况下,圆柱体积是圆锥体积的3倍。
等底等高的情况下,圆锥体积是圆柱体积的1/3
等底等高的情况下,圆锥体积比圆柱体积少2/3
等底等高的情况下,圆柱体积比圆锥体积多2倍
6、等体积等高的圆柱和圆锥,圆锥底面积是圆柱底面积的3倍;
等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍。
7、圆柱的横切:切成n段,需要n-1次,增加2×(n-1)个底面积
8、圆柱的纵切:切1次,增加2个长方形,长方形的长是底面的直径,宽是圆柱的高
9、圆锥的纵切:切1次,增加2个三角形,三角形的底是圆锥的直径,三角形的高是圆锥的高
10、把一个正方体削成一个最大的圆柱(或圆锥),正方体的棱长就是圆柱(或圆锥)的底面直径和高。
11、①熔铸(或铸成),体积不变。
②注水问题:上升的(或下降)的水的体积等于放入的的物体的体积。(完全 浸没)
12.一个圆柱的侧面展开图是一个正方形,
说明底面周长和高的比是1∶1,
半径和高的比是1∶2π,
直径和高的比是1∶π
13、当侧面积一定时,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
二、以数学小报的形式整理本单元知识 他山之石(图片来自网络,供同学们参考)