一种物理现象转化为另一种物理现象的转折状态叫临界状态。临界状态下的物理问题称为临界问题。解决临界问题的方法称为临界法。往往都是从临界态的情形入手去解决问题,具体看后面分析。在高中物理的各个部分都有临界问题。
比如,
一、静力学中的临界问题:平衡物体的临界状态是指物体所处的平衡状态将要被破坏而尚未被破坏的状态。
解决临界问题的关键是找到临界条件。物理方法:物理方法是指充分利用物理状态和物理规律,分析临界状态或边界条件,在特殊状态下,根据物理规律列方程,便可直接解决临界问题。
物理方法包括(1)利用临界条件,(2)利用边界条件,(3)利用矢量图。
临界问题与极值问题是相关联的,其主要区别是:临界问题通常用物理方法,极值问题通常用数学方法。具体举例看后面图片。
再比如,
动力学中的临界问题
动力学中的临界问题,临界条件主要有下列几种:
(1)接触与脱离的临界条件:两物体间的弹力
(2)相对滑动的临界条件:静摩擦力达到最大值
(3)绳子断裂与松弛的临界条件:断裂:绳中张力等于它所能承受的最大张力,松弛:
(4)加速度最大与速度最大的临界条件:在变化的外力作用下,物体所受合外力最大时加速度最大,所受合外力最小时加速度最小;加速度为0时,速度往往最大。
再比如,
圆周运动中的临界问题
(1)水平面上圆周运动的临界问题
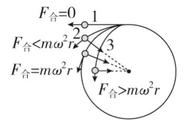
物体放在转动的圆盘上,随圆盘一起做匀速圆周运动,静摩擦力通过向心力。
物体相对圆盘恰好不发生相对滑动的临界条件是:最大静摩擦力恰好提供向心力,
即临界角速度。当圆盘转动的角速度时,物体将做离心运动。
例题4:联动轮摩擦力提供向心力的问题
(2)竖直平面内的圆周运动的临界问题
轻绳模型和轻杆模型在最高处受力临界情况,绳子物体最高处的向心力最小为物体重力,而杆模型最高处最小向心力为0。
再比如,
电磁感应中的临界问题
往往会有棒运动到最终匀速运动情况,这时候用的就是平衡方程求解。或者棒变减速运动到最终停止。等等情形。往往会用到能量方法。通常用到动能定理。动能定理与能量守恒是一致的。在动能定理中,能量的转化用功来体现,其中克服安培力做功等于机械能转化为电能再转化为内能即焦耳热。
“电磁感应”题中的“焦耳热”问题,又是高考题中常出现的问题。
所谓“焦耳热”,就是电流产生的热量,“电磁感应”中的“焦耳热”,是感应电流产生的热量。“焦耳热”的求法通常有3种:
一是直接法,根据公式求解;
二是间接法,应用动能定理或能量守恒定律求解。
三是用功与功率的关系求解。本题用第二种方法。
还要注意:题目是求电阻R上产生的热量,还是回路总的总焦耳热。
在与电磁感应有关的能量转化与守恒的问题中,要明确什么力做功与什么能的转化的关系,它们是:
合力做功=动能的改变;
重力做功=重力势能的改变;重力做正功,重力势能减少;重力做负功,重力势能增加;
弹力做功=弹性势能的改变;弹力力做正功,弹性势能减少;弹力做负功,弹性势能增加;
电场力做功=电势能的改变;电场力做正功,电势能减少;电场力做负功,电势能增加;
安培力做功=电能的改变, 安培力做正功,电能转化为其它形式的能;安培力做负功(即克服安培力做功), 其它形式的能转化为电能.
等等,具体分析请看图片