精确公式中的积分是椭圆积分,计算结果不能用初等函数表示。近似公式就是用级数展开得到的。
为了解决椭圆积分的问题,一大批数学家费尽心思创立了椭圆函数。
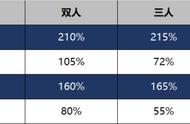
但是,结果有什么明显的差距吗?
而且,只要你愿意,还可以用级数展开得到精确度更高的近似公式。
多说一句,椭圆函数是19世纪最辉煌的数学成就之一,虽然在具体计算的时候用处不大,但这并不影响椭圆函数的伟大。
单摆很简单吗?

那它的周期怎么算?
大部分人知道的公式是这个:

但是,这只是摆角小于5度时的近似公式。
精确的周期公式是这样的:

公式中的积分也是椭圆积分
用级数展开的方法可以算出: