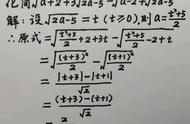例 化简^4√(7 4√3)- ^4√(7-4√3).
分析:如果直接从化简、计算的角度入手,则简直就是无从下手,而导致无从下手的原因是被开方数7 4√3与7-4√3被四次根号阻断。从方程角度出发,利用换元法可以打破这种局面。
解:设^4√(7 4√3)=a,^4√(7-4√3)=b,
则a^4 b^4=7 4√3 7-4√3=14,
ab=^4√[(7 4√3)(7-4√3)]=1,
由a^4 b^4=14,得
(a^2 b^2)^2-2 a^2b^2=14,
所以(a^2 b^2)^2=14 2(ab)^2=14 2=16,
因为a^2 b^2>0,
所以a^2 b^2=4,
即(a-b)^2 2ab=4,
所以(a-b)^2=2,
显然,a-b>0,
所以a-b=√2,
即^4√(7 4√3)- ^4√(7-4√3)=√2.
练一练:化简下列各式:
(1)√(2 √3)- √(2-√3)。
(答案:√2)
(2)^4√(17 12√2) ^4√(17-12√2).
(答案:2√2)
(3)^3√(26 15√3) ^3√(26-15√3).
(答案:4)
,