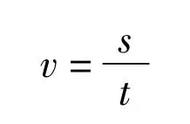考虑这颗星球所有可能的形状,怎样的形状才会让星球表面的某一点重力加速度达到最大?最大值是多少?
下图就是让表面某处的重力加速度达到最大的星球形状。这个图形是一个稍微有些变形的球体,整个图形是一个以 z 方向为轴的旋转体,顶端的 m 点即是重力加速度最大的点,它的重力加速度为 g = (4/5)(15/4)1/3π2/3M / V2/3,只比球形星体的重力加速度大 2.6% 。这是又一个经典的例子——圆形似乎并不是那么完美。

这个问题的解法非常漂亮。
首先,假设我们想要让星体表面上的某个点 m 的重力加速度最大,并且所受重力方向在 z 轴上,那么这个星体必然是沿 z 轴方向对称的。否则,取出不对称的一层,把多的部分填进少的部分让它变成一个完全对称的圆盘,这将会让 m 点在竖直方向上的受力变大。不断这样做直到这个图形沿 z 轴完全对称,显然就得到了一个更优的形状。
接下来的步骤就真的神了。
现在,在星体上取一个非常细的圆环,假设它的质量是 dM 。那么,这个圆环所贡献的重力加速度大小就是 G·dM·cosθ /r2 。如果把这个圆环从星体中挖掉,放到其它的位置上,那么新的圆环将会有新的 r 值和 θ 值。当整个形状达到最优时,这个形状将位于“极值点”的位置,也就是说它的“微分”为 0 ,任何微小的变动都不会改变 m 的加速度。
这就意味着, cosθ / r2 是一个常数。这个条件就确定出整个星体的形状。
问题五:
上楼时,人克服重力做功,需要耗费很多能量。但是,在平地上行走时,人并没有做功。那么,为什么我们走路时还要耗费能量呢?
1999 年 3 月的 Scientific American 上说到,其实在步行时,我们也是要克服重力做功的。这是因为,在步行的过程中,人的重心会一上一下地摆动。当两腿一前一后着地时,人的重心偏低;而单腿着地迈步时,人的重心会升高大约 3cm 。

我们走路的能量主要就消耗在了这里。
当然,事实上,即使人不走路,光是原地站着,也是要耗费能量的(大约为 80W )。假设人的步行速度是 v ,那么步行所用的能量可以用公式 P = 80W K·v 大致算出,其中 K·v 就是步行过程中耗费的能量,系数 K 大约为 160N 。
教中学物理最怕聪明孩子,一些古怪的问题常常会让老师也支支吾吾答不上来。
走路不做功,为什么还要耗费能量?电流从电厂来又回到电厂去,为什么我们还要支付电费?把装满水的水杯不盖纸片直接倒过来,为什么大气压没有把水支撑起来?拳头打在墙上后将会受到墙给拳头的反作用力,但若拳头挥空了,这个力的反作用力是什么?
这些,你都打算怎么解释?

不知道聪明的你今晚还能不能睡着?
本文作者:matrix67
“超级数学建模”(微信号supermodeling),每天学一点小知识,轻松了解各种思维,做个好玩的理性派。60万数学精英都在关注!
,