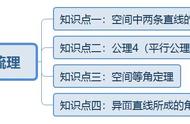
直线与直线位置关系的判断方法

(1)平行:当两条直线l1和l2的斜率存在时,l1∥l2⇔k1=k2;如果直线l1和l2的斜率都不存在,那么它们都与x轴垂直,则l1∥l2.
(2)垂直:垂直是两直线相交的特殊情形,当两条直线l1和l2的斜率存在时,l1⊥l2⇔k1·k2=-1;若两条直线l1,l2中的一条斜率不存在,另一条斜率为0时,则它们垂直.
(3)相交:两直线相交的交点坐标可由方程组的解求得.

判断两条直线的位置关系时要注意的两个易错点:一是忽视直线的斜率不存在的情况,二是忽视两直线重合的情况.解答这类试题时要根据直线方程中的系数分情况进行讨论,求出结果后再回代到直线方程中进行检验,这样能有效地避免错误.
圆的方程的求法(1)几何法,即通过研究圆的性质进而求出圆的基本量:如圆中弦所在的直线与圆心和弦中点的连线相互垂直;设圆的半径为r,弦长为|AB|,弦心距为d,则r2=d2+2(|AB|)等.
(2)代数法,即设出圆的方程,用待定系数法求解.在求圆的方程时,要根据具体的条件选用合适的方法,但一般情况下,应用几何法运算较简捷.

(1)直接求出直线与圆的交点坐标,利用两点间的距离公式求得;
(2)不求交点坐标,利用一元二次方程根与系数的关系得出,即设直线的斜率为k,直线与圆联立消去y后得到的方程的两根为x1、x2,则弦长d=|x1-x2|;
(3)利用半弦长、弦心距及半径构成的直角三角形来求.

在将方程变形时应时时注意变量的取值范围的变化,必须进行等价变形,这样才不会出错.
求动点轨迹时应注意它的完备性与纯粹性,求出方程后要对照图象进行检验.
,我是【学一点数学】,希望我的回答能给大家带来帮助。欢迎转发、评论,让更多人收益!