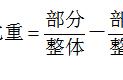第六节 比重
基本术语:
比重:指部分在整体中所占的比率,有时也用贡献率、利润率等表述方式。
增长贡献率:指部分增量在整体增量中所占的比例。
资料分析中的利润率特指利润在收入中的占比。
一、现期比重
1.识别:“……占……”(男生占全班的比重为多少);“……中……的占比”(全班中男生的占比为多少)。 男生是部分,全班是主体, 出现占字,占前/占后。
2.公式:
(1)比重=部分/总体。男 30 人,全班 100 人,求男占全班的比重=部分/总体=30/100=30%,全班除了男生就是女生,则女生占 70%。
(2)部分=总体*比重。全班 100 人,男生占全班的 30%, 求男生的人数:100*30%=30。
(3)总体=部分/比重。男 30 人,占全班的 30%, 求全班的人数: 30/30%=100。
(4)记忆:部分用乘法,总体用除法。
3.注意(设坑点):部分和总体的属性相同。 如:问男生的身高占全班的比重是多少?没说占全班的什么,但要注意,分子分母都要对应身高,属性必须对应。
4.引申概念:
(1) 增长贡献率:在全部的增长量中,一个小部分占的增长率。 增长贡献率=部分的增长量/总体的增长量。
例 1: 2017 年某地区 GDP 增长了 100 亿元,其中第一产业 GDP 增长了 20 亿元。第一产业为部分,增长 20 亿,总体即整体 GDP 增长 100 亿, 则第一产业对于总体的增长贡献率为 20%。
例 2:全家人一年共比去年多收入 10 万块钱,其中爸爸占 8 万,则爸爸对于全家的增长贡献率为 80%。
(2)利润率=利润/收入。 注意与数量关系不同,资料分析中分母是收入,数量关系中分母是成本。 因为数学运算题是理想情况,成本已知,但资料分析中,成本很难核算。
例: 2017 年某企业实现主营业务收入 100 万元,其中利润总额为 10 万元,则营业利润率为 10%(即: 在收入中,利润所占的比重是多少)。
【知识点】饼形图:
1.十二点钟原则: 十二点钟方向,顺时针依次排布。
2.若有总体(已经告知总体量为多少),先看部分占总体的特殊比重。如:已知一二三年级分别有 300、 200、 500 人,全校总人数有 1000 人,三年级占全校的比重为 500/1000=1/2,刚好占一半,找到饼状图第三个部分刚好占全部饼图一半的选项。
3.若无总体,看各部分之间倍数关系。
二、基期比重
1.识别:求上一年的比重/过去的比重。
2.公式:基期比重=A/B*(1 b)/(1 a)。
(1)A:部分的现期量;B:总体的现期量。
(2)a:部分的增长率;b:总体的增长率。
3.已知2017年(现期)的部分量A、总体量B、部分增长率a、总体增长率b,求2016年比重。2016年比重=2016年部分/2016年总体=[A/(1 a)]÷[B/(1 b)]=[A/(1 a)]*[(1 b)/B]=A/B*(1 b)/(1 a)。a和b都带着符号计算。
4.例:2017年进出口总额27万亿,同比增长14%,其中进口12万亿,同比增长19%。求:2016年进口所占比重。 A.42.6% B.44.4% C.48.6% D.51.2%
答:直接代入数据,A/B*(1 b)/(1 a)=12/27*(1 14%)/(1 19%)。计算时,先算前面分数,再估算后面分数,12/27=4/9,根据1/9≈11.1%,4/9≈44.4%,所以12/27≈44.4%。再看后面的,(1 14%)/(1 19%),分子小于分母,则(1 14%)/(1 19%)=1-,12/27*(1 14%)/(1 19%)=44.4%*1-<44.4%,对应A项。
注意:如果是下降14%,计算中变成(1-14%),带着符号计算。基期比重题目会有99%的题目存在现期比重的坑(选项中有现期比重的值),因为如果没有看清时间,会误认为是计算现期,所以“以坑治坑”,先算现期比重A/B,再看(1 b)/(1 a)与1的大小关系。
5.速算:
(1)先截位直除A/B。
(2)再看(1 b)/(1 a)与1的关系(>,<,=),结合选项选答案。
三、两期比重
【知识点】 两期比重比较——升降(套路题):
1.题型识别: 两个年份,一个比重,问“升降”。 如:基期比重是 45%, 现期比重是 50%,则现期比重上升;如果基期是 50%,现期是 45%,则现期比重下降。
2.例:2017年小麦产量为A万吨,同比增长率为a,2017年粮食产量为B万吨,同比增长率为b,则2017年小麦产量占粮食产量的比重相对于去年上升还是下降?
推导:判断比重升/降,做减法,2017年比重-2016年比重,大于0比重上升,小于0比重下降。2017年比重=A/B,2016年比重为基期比重=A/B*(1 b)/(1 a),2017年比重-2016年比重=A/B-A/B*(1 b)/(1 a)=A/B*[1-(1 b)/(1 a)]=A/B*(1 a-1-b)/(1 a)=A/B*(a-b)/(1 a)。看与0的关系(大于0还是小于0):A和B都是产量,则A/B一定为正;再看1 a,当a>0时,1 a为正,a<0时,现在是资料分析题目,不可能出现某个产业的增长率是-100%,而且公务员考试中,不可能考出现泡沫经济的情况,所以1 a一定大于0。所以正负由a-b决定:如果a-b>0,即a>b,现期比重上升;a-b<0,即a<b,现期比重下降;a=b,比重不变。
3.公式:现期比重-基期比重=A/B-A/B*(1 b)/(1 a)=A/B*(a-b)/(1 a)。
4.升降判定:记住结论即可。
(1)a>b,现期比重上升。
(2)a<b,现期比重下降。
(3)a=b,比重不变。
(4)a:分子(部分)的增长率;b:分母(总体)的增长率。
5.注:比较时增长率带着正负号进行比较。
6.如:上海GDP增长13%,全国GDP增长7.8%,则上海(部分)占全国的比重上升。
7.a是部分增长率,对应分子;b是总体增长率,对应分母。
【知识点】两期比重计算——上升、下降 百分点。百分点是两个百分数相减的结果,即求现期比重-基期比重的结果。
1.示例:2017年小麦产量为A万吨,同比增长率为a,2017年粮食产量为B万吨,同比增长率为b,则2017年小麦产量占粮食产量的比重相对于去年上升、下降多少个百分点?
推导:与之前相同,略过。
2.公式:
现期比重-基期比重=A/B*(a-b)/(1 a)=A/B*1/(1 a)*(a-b)<|a-b|。
A/B是一个比重,不到100%,则A/B=1-;
当a>0时,1/(1 a)=1-,
当a<0时,考试中A/B*1/(1 a)=1-,所以资料分析中,A/B*1/(1 a)结果一定等于1-。
A/B*1/(1 a)*(a-b)=1-*(a-b),结果一定比a-b小。
3.方法:
(1)判方向:a>b上升,a<b下降。
(2)定大小:两期比重差<|a-b|。
4.野路子:判方向,选最小(实在不行,截位计算)。
【小结】比重梳理:
1.现期比重:占→占前(A)/占后(B)=部分/总体。
2.基期比重:占,基期→A/B*(1 b)/(1 a),交叉乘。
3.两期比重:
(1)比重,升降→a大升;a小降。
(2)比重,百分点→先判升降,再选小。

【小结】比重
1.现期比重:
(1)识别:问题时间与资料一致,占,比重。
(2)公式:比重=部分/整体;整体=部分/比重;部分=整体*比重。
(3)速算:截位直除。
2.基期比重:
(1)识别:问题时间在资料之前,占,比重。
(2)公式:A/(1 a)÷[B/(1 b)]=A/B*[(1 b)/(1 a)]。
(3)速算:①截位直除;②先计算现期比重,再判断大小。
3.两期比重:
(1)识别:两个年份,一个比重。
(2)公式:A/B*[(a-b)/(1 a)]。
(3)升降判断:比较部分与整体增长率,部分大则升,小则降。
(4)速算:比重差小于增长率之差,即|A/B*[(a-b)/(1 a)]|<|a-b|。
第七节平均数
一、现期平均数
【知识点】现期平均数(总体平均到几个部分):
1.题型识别:问题时间与材料时间一致 平均(均、每、单位)。如单位面积人口,是每平方米有几个人。大家都说中国的居住环境很差,其实和日本、韩国相比,中国的单位面积人口没有他们多。
2.例:2017年棉花产量A吨,种植面积为B亩。问:2017年棉花平均亩产(吨/亩)?
答:出现“平均”,是平均数问题。“平均亩产”的“产”在后面,“亩”在前面,则平均数=总产量/总面积=A吨/B亩。或者看单位,分子是吨,分母是亩,这就是用意义列式。
3.公式(能够快速列式):平均数=总数/个数=A(分子)/B(分母)=后/前(平均数喜欢用倒装语序)。
(1)例:都是后/前,如人均收入=收入/人数;每亩的产量=产量/亩数;单位面积产量=产量/面积。可以用“均”做一个界限,最后出现的是分子,前面出现的是分母。
(2)速算:截位直除。注意单位,计算结果可能是特别大的数字,要看材料单位和选项单位是否一致,如吨/亩、万吨/公顷。
【知识点】削峰填谷:
1.适用题型:平均数的计算或比较(未给总数)。
2.方法:
(1)划线(找一个相对居中好算的数——整数):找峰、谷。
(2)计算:用峰填谷,基准线 剩余的和/n。怎么理解:沙滩玩沙子,堆一个沙包,用手抹平,抹平的过程就是削峰填谷。
3.例:求420、260、380、410、520、470平均数。
答:求平均数不要全部相加,再除以6。找一个比较整的中间数字,如把400看成基准线,峰谷分别为 20、-140、-20、 10、 120、 70,全部相加为60,再平均一下(不是一个数剩余60,是整体剩余60),60/6=10,推出平均数=400 10=410。
二、基期平均数
【知识点】基期平均数——给增长量:
1.题型识别:问题时间在材料时间之前 平均(均、每、单位)。
2.例:2017年棉花产量A,较上年增长50吨,种植面积为B,较上年增长10亩。问:2016年棉花平均亩产?
答:平均数=2016年产量/2016年面积=(A-50)/(B-10)。
【知识点】基期平均数——给增长率:
1.题型识别:问题时间在材料时间之前 平均(均、每、单位)。
2.基期平均数(与基期比重公式相同)=A/B*[(1 b)/(1 a)]。A:总数现期量;B:个数现期量;a:总数增长率;b:个数增长率。
3.例:2017年棉花产量A,较上年增长a,种植面积为B,较上年增长b。问:2016年棉花平均亩产?
答:平均数=2016年产量/2016年面积=A/(1 a)÷[B/(1 b)]=A/B*[(1 b)/(1 a)]。先算现期平均数,再根据后面“小尾巴”与1的大小选答案。
4.速算:
(1)截位直除(多步除法,上下都截)。
(2)先截位直除A/B,再看(1 b)/(1 a)与1的关系(>,<,=),结合选项选答案。
三、两期平均数
【知识点】两期平均数——比较(与两期比重的比较结论一样):
1.识别:两个时期 平均数 上升/下降。
2.例:S市2017年房屋销售金额为A,比上年增长30%;房屋交易面积为B,比上年增长10%。问:2017年S市房屋均价较上年上升?下降?
答:可以这样理解:钱增长30%,交易面积增长10%,面积的增长没有跟上钱的增长,是涨价了,即房屋均价较上年相比是上升了。或者a=钱的增长率,b=面积的增长率,a>b,上升。
3.方法:比a(总数增速)和b(个数增速)大小:
(1)a>b,今年上升。
(2)a<b,今年下降。
(3)a=b,今年不变。
【知识点】两期平均数——计算(平均数的增长率,基本每次考试都考):
1.识别:两个时期 平均 上升/下降 百分之几。
如老师所在地区2018年房价的均价是1.3万,2019年是1.5万,则平均房价的增长率=(1.5-1.3)/1.3。考试一般给成交金额和面积,单价需要自己计算。
2.例:2015年1~5月B区规模以上文化创意产业从业人员人均完成收入约比上年同期增长:
A.2.5%B.8.4%C.10.8%D.13.4%
答:在一个时间段,人均……比上年增长 %,即求平均数的增长率。
3.公式:平均数的增长率=(a-b)/(1 b)。
4.注意:
(1)a、b要带正负号。
(2)按照公式计算!没有野路子。
5.公式推导:
2017年棉花产量A,较上年增长a,种植面积为B,较上年增长b。问:2017年棉花平均亩产增长()%?答:平均数增长率=(现期-基期)/基期=现期/基期-1=A/B÷{A/B*[(1 b)/(1 a)]}-1=(1 a)/(1 b)-1=(1 a-1-b)/(1 b)=(a-b)/(1 b)。公式推导没有意义,绝对不会考,主要是代入数据计算。注意分母是(1 b),大家死记硬背记下来,如老师到死都不会忘记困难的单词怎么写,因为小学时写错了,老师让抄了50遍。
【知识点】两期平均数——平均数的增长量(选学,考得很少,稍微听一下即可。因为2017年有几个省份考过,所以还是讲一下):
1.识别:两个时期 平均 增长(单位)。如今年房屋均价是1.5万,去年是1.3万,则平均数的增长量=1.5-1.3=0.2万。
2.例:2015年1~5月B区规模以上文化创意产业从业人员人均完成收入约比上年同期增长:
A.250元B.184元C.1008元D.1340元
答:时间是现期,平均数 增长 单位,求平均数的增长量。
3.公式:平均数的增长量(也是两期比重差公式)=A/B*[(a-b)/( a)],一般分子、分母截两位估算。
4.注意:
(1)a、b要带正负号。
(2)公式和两期比重计算公式完全一致。
5.公式推导:现期平均数-基期平均数=A/B-A/B*[(1 b)/(1 a)]=A/B*[(a-b)/(1 a)]。

【小结】平均数知识点梳理:
1.识别考点:平均、每→后/前。
2.注意分母:平均几次,除几次。
3.没给总数:削峰填谷。
4.基期平均数:老套路,A/B*[(1 b)/(1 a)]。
5.两期平均数:
(1)升降看a、b(老套路)。
(2)增长率公式:(a-b)/(1 b)。
(3)增长量公式:A/B*[(a-b)/(1 a)]。

【小结】平均数:
1.现期平均数:
(1)识别:问题时间与资料一致 平均(均/每/单位)。
(2)公式:平均数=总数/个数=后面/前面。
(3)技巧:①截位直除;②削峰填谷。
2.基期平均数:
(1)识别:问题时间在资料之前 平均(均/每/单位)。
(2)公式:A/(1 a)÷[B/(1 b)]=A/B*[(1 b)/(1 a)]。
(3)速算:①截位直除;②先计算现期平均数,再判断大小。
3.两期平均数:
(1)识别:题干中涉及两个时间 平均(均/每/单位)。
(2)升降判断:看分子、分母增长率,分子大则升、小则降。
(3)平均数的增长率:(a-b)/(1 b)。
(4)平均数的增长量:A/B*[(a-b)/(1 a)]。
第八节倍数
基本术语:倍数用来表示两者的相对关系。若A是B的n倍,则n=r 1(r指A与B相比的增长率)。
【注意】倍数相关(注意经常在文字部分设坑,知识点不难):
1.现期倍数:
(1)是几倍。
(2)多几倍=是几倍-1,注意需要-1。
2.基期倍数。
【知识点】倍数:
1.识别:时间 倍数(比、比例)。
2.公式:
(1)现期倍数:
①A是B的几倍:A/B;
②A比B多(增长)几倍:(A-B)/B=A/B-1。
(2)基期倍数:A/B*[(1 b)/(1 a)]。
3.速算:
(1)截位直除(多步除法,上下都截)。
(2)先截位直除A/B,再看(1 b)/(1 a)与1的关系。
一、现期倍数
【知识点】现期倍数:
1.题型识别:问题时间与材料时间一致,A是B的几倍。
2.例:2017年棉花产量A,大豆产量B。问:2017年棉花产量是大豆的几倍?
答:倍数=A/B。
【知识点】倍数VS多几倍(增长率):
1.题型识别:A比B多几倍。
2.(1)A是B的几倍:A/B。
(2)A比B多几倍(增长率):A/B-1。
(3)A超过B的n倍:“超过”即大于,A>B*n,即A/B>n。
二、基期倍数
【知识点】基期倍数:
1.题型识别:基期 倍数。
2.基期倍数:A/B*[(1 b)/(1 a)]。
3.例:2017年棉花产量A,较上年同期增速为a;大豆产量为B,较上年同期增速为b。问:2016年棉花产量是大豆的几倍?
4.速算:
(1)截位直除(多步除法,上下都截)。
(2)先截位直除A/B,再看(1 b)/(1 a)与1的关系。

【小结】比重、平均数、倍数问题考点辨析(注:a代表分子增长率,b代表分母增长率):
1.比重(占、比重):
(1)现期:A/B。
(2)基期:A/B*[(1 b)/(1 a)]。
(3)升降判断:
①a>b,比重上升;
②a<b,比重下降;
③a=b,比重不变。
(4)定量计算:两期比重差=A/B*[(a-b)/(1 a)],先升降,再选小。
2.平均数(均、每、单位):
(1)现期:A/B。
(2)基期:A/B*[(1 b)/(1 a)]。
(3)升降判断:
①a>b,平均数上升;
②a<b,平均数下降;
③a=b,平均数不变。
(4)平均数的增长率=(a-b)/(1 b)。
3.倍数:
(1)现期:A/B。
(2)基期:A/B*[(1 b)/(1 a)]。

【小结】倍数:
1.现期倍数:
(1)识别:问题时间与资料一致,A是B的多少倍。
(2)公式:A/B。
(3)速算:截位直除。
2.基期倍数:
(1)识别:问题时间在资料之前,A是B的多少倍。
(2)公式:A/(1 a)÷[B/(1 b)]=A/B*[(1 b)/(1 a)]。
(3)速算:①截位直除;②先计算现期倍数,再判断大小。
3.倍数问法:
(1)A是B的n倍:n=A/B。
(2)A比B增长(多)r倍:r=A/B-1。
【注意】作业梳理:
1.比重:关键字:占。
(1)现期比重:比重=部分/总体、部分=总体*比重、总体=部分/比重。
(2)基期比重:
①公式:A/B*[(1 b)/(1 a)]。
②速算:先算A/B,B截三位;再估算(1 b)/(1 a)与1的关系(>,<,=)。
(3)两期比重比较:一句话:看a和b的大小,a>b,比重上升;a<b,比重下降;a=b,比重不变。
(4)两期比重计算:第一步,判方向;第二步,选小的。
2.平均数:关键字:“平均”“每”。核心是判断题型,找分子、分母。
(1)现期平均:
①平均数=后/前;注意:日均、月均的表述。
②削峰填谷:第一步,找到基准线;第二步,用峰去填谷。
(2)基期平均:
①公式:基期平均=后/前。
②速算:先算A/B,B截三位;再估算(1 b)/(1 a)与1的关系(>,<,=)。
(3)两期平均比较:一句话:看a和b的大小,a>b,比重上升;a<b,比重下降;a=b,比重不变。
(4)两期平均计算:公式:(a-b)/(1 b)。两期平均数增长量:A/B*[(a-b)/(1 a)]。
3.倍数:关键字:倍、多几倍、某几个量的比例关系。
(1)现期倍数:
①是几倍=A/B;多几倍=A/B-1。
②A超过B的N倍→A>B*N。
(2)基期倍数:
①公式:A/B*[(1 b)/(1 a)]。
②速算:先查找(查出第一个是分子,第二个是分母),再计算比例。
,