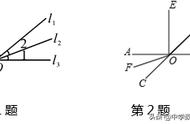
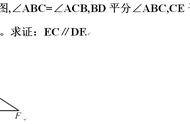在同一平面内,如果两条直线a和b不相交,我们就称这两条直线平行,记作a∥b。
上节课我们学习了相交线,这节课我们学习平行线。在同一平面内,两条直线的位置关系要么相交,要么平行。
平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
即如果b∥a,c∥a,b∥c。
那么,我们怎样判定两条直线平行呢?
判定方法1.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行。
简称:同位角相等,两直线平行。
判定方法2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
简称:内错角相等,两直线平行。
判定方法3.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
简称:同旁内角互补,两直线平行。

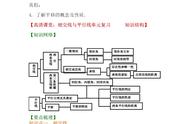
平行线的判定
我们通常就是用这三种判定方法来判定两条直线是否平行。
,