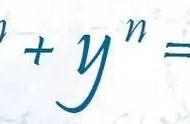费马大定理,又称费马最后定理,是一道由法国数学家皮埃尔·德·费马在17世纪提出的问题。它的正式陈述是:对于大于2的任何正整数n,方程x^n y^n = z^n没有正整数解。这个问题的提出已经有358年的历史,它曾经困扰了无数数学家,直到20世纪才被英国数学家安德鲁·怀尔斯证明。

费马大定理是数学史上最著名的问题之一,它涉及到整数解的概念,具有重要的理论意义和实际应用价值。尽管这个问题已经有358年的历史,但由于证明难度极大,因此直到20世纪才被证明。在这之前,许多著名的数学家都曾经尝试证明这个问题,但都没有成功。

怀尔斯的证明使用了一些新的数学工具和方法,例如椭圆曲线、模形式等,他的证明被认为是数学史上最重要的成果之一。怀尔斯的证明不仅解决了费马大定理这个问题,而且还推动了许多其他领域的数学研究,例如代数几何、代数拓扑等。

尽管费马大定理已经被证明,但它仍然是数学界最具挑战性和吸引力的问题之一。它涉及到整数解的概念,以及一些基本的数学概念和技巧,因此它对于推动数学的发展和应用都具有重要的意义。
,