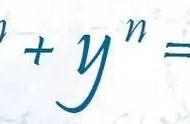皮耶·德·费马(Pierre de Fermat)是一个17世纪的法国律师,也是一位业余数学家。之所以称业余,是由于皮耶·德·费马具有律师的全职工作。他在数学上的成就不比职业数学家差,他似乎对数论最有兴趣,亦对现代微积分的建立有所贡献。著名的数学史学家贝尔(E. T. Bell)在20世纪初所撰写的著作中,称皮耶·德·费马为”业余数学家之王“。贝尔深信,费马比皮耶·德·费马同时代的大多数专业数学家更有成就。17世纪是杰出数学家活跃的世纪,而贝尔认为费马是17世纪数学家中最多产的明星。

费马生于法国南部,在大学里学的是法律,以后以律师为职业,并被推举为议员。费马的业余时间全用来读书,哲学、文学、历史、法律样样都读。30岁时迷恋上数学,直到他64岁病逝,一生中有许多伟大的发现。不过,他极少公开发表论文、著作,主要通过与友人通信透露他的思想。他的很多成果都是在他死后,由他儿子通过整理他的笔记和批注整理出来的。好在费马有个“不动笔墨不读书”的习惯,凡是他读过的书,都有他的圈圈点点,勾勾画画,页边还有他的评论。他利用公务之余钻研数学,并且成果累累。后世数学家从他的诸多猜想和大胆创造中受益匪浅,赞誉他为“业余数学家之王”。
费马对数学的贡献包括:与笛卡尔共同创立了解析几何;创造了作曲线切线的方法,被微积分发明人之一牛顿奉为微积分的思想先驱;通过提出有价值的猜想,指明了关于整数的理论——数论的发展方向。他还研究了掷骰子赌博的输赢规律,从而成为古典概率论的奠基人之一。
其中最为出名的是——费马大定理 (费马大定理:n>2是整数,则方程x^n y^n=z^n没有满足xyz≠0的整数解。这个是不定方程,它已经由英国数学家怀尔斯证明了(1995年),证明的过程是相当艰深的!)。这个猜想最初出现费马的《页边笔记》中,费马在阅读丢番图(Diophatus)《算术》拉丁文译本时,曾在第11卷第8命题旁写道:“将一个立方数分成两个立方数之和,或一个四次幂分成两个四次幂之和,或者一般地将一个高于二次的幂分成两个同次幂之和,这是不可能的。关于此,我确信已发现了一种美妙的证法 ,可惜这里空白的地方太小,写不下。”(拉丁文原文文: "Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.")毕竟费马没有写下证明,而他的其它猜想对数学贡献良多,由此激发了许多数学家对这一猜想的兴趣。

数学家们的有关工作丰富了数论的内容,推动了数论的发展。尽管费马同时表明他已找到一个绝妙的证明而页边没有足够的空位写下,但仍然经过数学家们三个多世纪的努力,猜想才变成了定理。为了获得它的一个肯定的或者否定的证明,历史上几次悬赏征求答案,一代又一代最优秀的数学家都曾研究过,即使用现代的电子计算机也只能证明:当n小于等于4100万时,费马大定理是正确的。在冲击这个数论世纪难题的过程中,无论是不完全的还是最后完整的证明,都给数学界带来很大的影响;很多的数学结果、甚至数学分支在这个过程中诞生了,包括代数几何中的椭圆曲线和模形式,以及伽罗瓦理论和赫克代数等。这也令人怀疑当初费马是否真的找到了正确证明。而安德鲁·怀尔斯由于成功证明此定理,获得了2005年度邵逸夫奖。
一个业余数学家,在平时阅读写下的一句话,让后世专业的数学家研究了三个多世纪!(很多人怀疑当初他想到的证明方法到底存不存在)。
关于费马有没有证出费马大定理,而『我确信我已经找到了一个美妙的证法,可惜这里地方太小,写不下。』