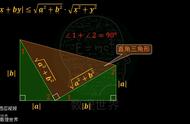
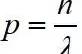不等式起源于19世纪的西欧,所以不等式的抽象能力较大,数学公式非常简洁,但是阻碍了学习者进入数学领域,这也是自19世纪以来科学越来越高度抽象,需要从业者具有较高的抽象能力,美就在其中.
高中的不等式在必修5的第四章和选秀4-5不等式选修,这里面涉及到几十种不等式,但不等式的基础是8个公理,书写的形式与欧几里得先生的《几何原本》相同,公元前3世纪欧几里得先生的《几何原本》奠定了现代科学体系研究方法,即演绎推理.欧洲的文明不断地交替更迭,但是科学研究的方法却一脉相承,如果一个文明一成不变,那么只能说明该文明科学落后,在一个文明中起的作用很小,甚至微乎其微.
不等式是高中阶段竞赛、自主招生以及强基计划的宠儿,难度不言而喻,那么到底谁才是高中阶段最美丽的不等式呢?
谁是高中阶段最美丽的不等式呢?是柯西不等式,美在何处呢?
柯西不等式是均值不等式、重要不等式以及经典不等式等一般形式.柯西不等式可以作为这些不等式证明的方法来研究问题柯西不等式从数量、图像以及向量多角度来阐述问题
一、经典不等式
经典不等式为调和均数、几何均数、算数均数以及平方和均数之间大小关系,不等式研究需要从“代数式结构”和“几何意义”两方面来研究,尤其“几何意义”才是学习和教学重点,艾萨克-牛顿先生是非常鄙视“笛卡尔先生的代数法解决几何问题”,可想而知:科学的数学本质是几何化,故几何是数学的花园;代数式结构需要从“不等式方向”、“取等条件”以及“要素之间的动态关系和静止关系”三方面来解读.
1.复习巩固

2.题型解析




二、高维柯西不等式

对于其他形式的不等式本文就不详谈了,若是有感兴趣的读者朋友可以私下讨论,科学家柯西先生是法兰西最伟大的数学家,其成就可以与德国的数学王子“高斯先生”比肩,有感兴趣的同学可以读一读其数学著作,但是柯西先生的人品是值得商榷,因为他间接断送了21岁的《抽象代数》和《群论》著作者---伽罗瓦,人类史上绝无仅有的超级天才.