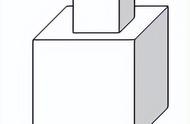
小川今年读六年级,前几天刚刚学习了长方体和正方体的表面积计算。一日,闲来无事,与他谈起把若干个同样的小正方体摆成不同长方体的话题。
我:用8个相同的小正方体摆成大长方体,有几种不同的摆法?
川:(想了一会儿)有三种拼法,第一种摆成1排;第二种摆成两排,前排4个,后排4个;第三种摆成2层,上层4个,下层4个。
我:如果把第二种摆法竖起来,它和第三种摆法是什么关系?
川:如果竖起来,后两种摆法其实就是一样的。
我:这么说的话,一共有几种不同的摆法?
川:两种。
我:确定没有其他摆法了?
川:确定。
出示用8个同样大的小正方体摆成的大正方体。
我:正方体也能看成长方体吗?
川:能。噢,一共有三种摆法,还可以摆成2×2×2的正方体。
我:这三种摆法摆成的长方体表面积相等吗?如果不等,表面积最小的是哪一种摆法?
川:应该不等。你等一会,我画个图算算看。
稍后,川指着图向我汇报。
川:第一种是8×1×1的长方体,第二种是4×2×1的长方体,第三种是2×2×2的正方体,它们的表面积分别是34、28、24,第三种表面积最小的原因是减少的面最多。
我:不仅算出表面积最小的摆法,还能分析背后的原因,很棒!那么,你还能想到什么?
川:用小正方体摆成大长方体,应该尽量摆成正方体,因为由于减少的面越多,摆成的长方体的表面积就越小。
我:先画出各种摆法的示意图,再根据各自的表面积得到最佳摆法,是一种常规的方法,比较耗时。我有一种快捷的方法,愿意听吗?
川:(兴奋地)愿意,愿意。
我:先用2个小正方体摆一摆,得到2×1×1的长方体,把这个长方体记作长方体①;然后用两个长方体①继续摆,要使表面积小,就要重叠大面,得到2×2×1的长方体,把这个长方体记作长方体②;最后用两个长方体②摆一摆,仍然重叠大面,得到2×2×2的正方体。这样直接得到摆成正方体时表面积最小,不需要画出各种不同的摆法,也不需要算出各自的表面积。
川:我懂了,每次重叠最大的面,就能保证摆成的大长方体的表面积最小。
我:(竖起大拇指表扬)是的!这就是摆出表面积最小的长方体的关键。
我:来点有挑战性的----如果用8个长3厘米、宽1厘米、高1厘米的小长方体摆成大长方体,怎样摆表面积最小?
川:(边画边说)先用2个长3厘米、宽1厘米、高1厘米的小长方体摆成3×1×2的长方体,把这个长方体记作长方体①;然后用两个长方体①摆成3×2×2的长方体,把这个长方体记作长方体②;最后用两个长方体②摆成3×2×4(或3×4×2)的长方体。

我:我们把上面的操作过程再理一理,第一次把上下两个面重叠,也就是把3×1的面重叠,高就由1厘米变成2厘米,于是得到3×1×2的长方体①;第二次把前后两个面重叠,也就是把3×2的面重叠,宽就由1厘米变成2厘米,得到3×2×2的长方体②……
川:(恍然大悟)我好像明白了,第三次把最大的面3×2重叠,另一个数据就会乘2变成4,得到3×2×4(或3×4×2)的长方体。
我:根据这个过程,如果不画图,你能按要求找出表面积最小的摆法吗?
川:能!就像刚才摆大长方体的过程,可以表示成下面这样。
3×1×1 3×1×2
3×2×2 3×2×4
我:你的意思是,每次变化中都有两个数不变,剩下的一个数乘2。不变的两个数有什么特点?
川:不变的是连乘算式中乘积最大的那两个数。例如,4×3×1中不变的就是4×3;5×3×4中不变的就是5×4。
我:这样做意味着每次要把哪两个面拼在一起?
川:这样做就表示每次都要把面积最大的两个面拼在一起,剩下的一个数乘2就表示宽或高扩大到原来的2倍。
……
用若干个同样的小正方体摆成表面积最小的长方体是“长方体和正方体”单元常见的操作活动之一,各版本教材中都有所涉及。但究竟怎么摆才能使摆成的长方体的表面积最小,我们通常会引导学生先画一画,再算一算。这样教学,尽管倍学生理解,但比较耗时费力,且容易发生遗漏(尤其是摆法较多的时候)。更重要的是,学生在此过程中缺少理性思维,题虽解了,但数学思维并没有得到充分的发展。基于此,笔者从侄儿已有的知识基础和思维能力出发,着力引导他经历“先画再算”、“只画不算”、“只算不画”这三个不同层次的活动过程,促使其思维从直观走向表象,从表象走向想象,在发现规律的同时不断发展其思维力。
第一层次,先画再算,纯直观,基于现实基础的思维起点。小学高年级是直观形象思维向抽象逻辑思维的过渡期。但是这个时期的儿童仍不能脱离直观形象思维,解题时依旧喜欢画图思考。用8个相同的小正方体摆成大长方体,怎么摆表面积最小?川的方法是先画再算。先画,明确有几种摆法;再算,知道哪种摆法摆成的长方体的表面积最小。
第二层次,只画不算,半直观,逐步把握问题的核心。基于小学高年级学生的认知特点,根据“每次重叠最大的面,就能保证摆成的长方体的表面积最小”,分布呈现相应的示意图,舍弃其他摆法,以及通过逐个计算进行比较的过程,大大节省了时间,提高了解题效率。这个层次的画图是一种“半直观”,是连接直观与抽象的桥梁。在这样的状态下,解题活动的目标不再仅仅局限于解决具体的问题,而是更多地着眼于发现规律,提升能力。
第三层次,只算不画,纯想象,思维水平得到真正的提升。在逐个观察示意图的过程中,引导学生逐步发现每次把最大的两个面重叠,就会使连乘算式中最小的数扩大到原来的2倍。在此背景下,不摆、不画,只要根据长、宽、高3个数据的大小就能推算出下次的摆法,从而得到更大长方体的相关数据。每次把最小的数据乘2,就会使长、宽、高3个数据之间的差距变小,这就暗合了“用同样的小正方体摆成大长方体,要使表面积最小,就要尽量摆成正方体或接近正方体的长方体”。如果说先画再算是思维的起点,只画不算是思维的拐点,只算不画就是思维的高点。因为在这个层次,学生能够完全摆脱直观的束缚,仅仅借助数据就能推出所要的摆法,进而使问题合乎逻辑地得以解决。
,