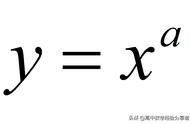在学完函数的概念和单调性之后,紧接着我们就开始来接触一些具体的函数。最先登场的便是幂指对,这三个函数可以说是函数中的三座大山,登过去了前面就开阔平坦,风景美好,一览无余,登不过去,那就可能会累死在半山腰。通过对这三个函数的学习,不仅仅可以使我们头脑中有一些具体的函数模型,以便我们对函数有更深刻的认识,同时,我们在这样一个过程中也会学习到一些函数性质,比如函数的奇偶性。所以,这三个函数在高中数学中的地位可想而知。
一:幂函数
幂函数是指形如y=xα(α为实数)的函数,其中x称为底数,也是幂函数的自变量,α称为指数。幂函数是一个函数种类,并且是一个非常重要的函数种类。幂函数在高考数学中有很大份量,在高等数学中有很大份量,在工业化应用中有很大份量;幂函数包含了数量丰富的各种函数,衍生出去,衔接了个数不菲的常用函数,譬如:一次函数、二次函数、正比例函数、反比例函数、根式函数、立方函数.. ...那么,幂函数的性质、规律、图像以及应用,自然而然就成为数学中一个非常吸引人的话题。
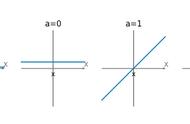
幂函数图像是性质好的反映,是规律好的呈现,是应用好的助手,影响幂函数图像的走向和形状的重要因素实际上是α。

虽然幂函数图像会因为α的改变而变。但其实它的图像具有一般性规律,幂函数图像一定遵循下面5点规律:
①任何幂函数图象一定经过第一象限;
②任何幂函数图像一定不经过第四象限;
③幂函数的图像可能经过第二象限、第三象限,这取决于这个幂函数的奇偶性;当幂函数为奇函数时,那么这个幂函数的图像经过第三象限,eg:f(x)=x3的图像;当幂函数为偶函数时,那么这个幂函数的图像经过经过第四象限,eg:f(x)=x2的图像;
④任何幂函数的图象最多只能同时出现在两个象限内;
⑤假如幂函数的图象与坐标轴相交,那么这个交点一定是原点。
二:指数函数
谈到指数函数,小朋友们首先想到的可能是指数爆炸。或者想到这样一个关于指数函数的例子:细胞的分裂是一个很有趣的现象,新细胞产生的速度之快是十分惊人的。例如,某种细胞在分裂时,1个分裂成2个,2个分裂成4个……因此,理想条件下第x次分裂得到新细胞数y与分裂次数x的函数关系式即为:y=2x。
一般地,函数y=ax(a为常数且以a>0,a≠1)叫做指数函数,函数的定义域是R。 对于一切指数函数来讲,值域为(0, ∞)。指数函数中ax
前面的系数为1。如:y=10x,,y=πx 都是指数函数;注意:y=3·2x前系数为3,故不是指数函数。
三:对数函数
我们知道,高中数学教科书是先讲指数,后以反函数形式引出对数的概念。但在历史上,恰恰相反,对数概念不是来自指数,因为当时尚无分指数及无理指数的明确概念。布里格斯曾向纳皮尔提出用幂指数表示对数的建议。1742年,J.威廉(1675-1749)在给G.威廉的《对数表》所写的前言中作出指数可定义对数。而欧拉在他的名著《无穷小分析寻论》(1748)中明确提出对数函数是指数函数的逆函数,和21世纪的教科书中的提法一致。
一般地,函数y=logaX(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数。其中x是自变量,函数的定义域是(0, ∞),即x>0。它实际上就是指数函数的反函数,可表示为x=ay。因此指数函数里对于a的规定,同样适用于对数函数。
以下是幂指对函数中涉及到的一些经典题目,敬请鉴赏。