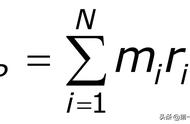转动惯量与离心力啥关系?
一、转动惯量(Momentum of Inertia)
1、质量转动惯量基本定义:
刚体绕轴转动时惯性(回转物体保持其匀速圆周运动或静止的特性)的量度,用字母I或J表示。
在经典力学中,转动惯量(又称质量惯性矩,简称惯矩)通常以I 或J表示,SI 单位为 kg·m²。
对于一个质点,
J(I) =1/2* mr²,
其中 m 是其质量,r 是质点和转轴的垂直距离。
2、动力学公式:
角动量L:质点动量p对O点之动量矩(通常称为角动量)L(O)(简记为L)
L=Iω, ω:刚体角速度。I:刚体转动惯量。
定轴转动动能E:
E=1/2*Iω2,
二、离心力(centrifugal force)
是一种虚拟力,是一种惯性的体现,它使旋转的物体远离它的旋转中心。
- 离心力的产生:
想象一个围绕中心旋转的圆盘,角速度为ω。在圆盘上有一个质量为m木块,木块由绳子连接,绳子的另一端固定在圆盘的中心(也是旋转中心),绳长为r。木块随圆盘一同转动,假设没有任何摩擦力,木块的旋转是由于绳子的拉力。在随圆盘一同转动的观察者看来,木块是静止的。
根据牛顿定律,木块受到的合力应为零。但是木块只受到一个力,就是绳子的拉力,所以合力不为零。那么这违反牛顿定律吗?
牛顿定律只有在惯性系下才成立,但是随圆盘一同转动的观察者所在的参考系是非惯性系,所以牛顿定律在这里不成立。为了使牛顿定律在非惯性系下仍然成立,那么就需要引用一个惯性力,即离心力。
离心力的大小为 ,与绳子提供的拉力相等,但方向与之相反。引入离心力后,在随圆盘一同转动的观察者看来,木块同时受到绳子的拉力和离心力,大小相等,方向相反,合力为零。此时木块静止,牛顿定律成立。
F离心力=m*ω2*r
- 相对离心力:
通常离心力常用地球引力的倍数来表示,因而称为相对离心力 “ RCF ”。或者用数字乘“g”来表示,例如25000×g,则表示相对离心力为25000。相对离心力是指在离心场中,作用于颗粒的离心力相当于地球重力的倍数,单位是重力加速度“g”(980cm/sec2),此时“RCF”相对离心力可用下式计算:
RCF = 1.119×10-5×(rpm)2* r ,单位:.g。 ( rpm — revolutions per minute每分钟转数,r:旋转半径,cm)