浮力的计算始终是中考的重点内容。本篇文章侧重介绍有关上提下拉类浮力计算题。这类题目除了要求熟练掌握浮力的基础知识(浮力的四种计算方法、物体的浮沉条件等),还要会用隔离法分析物体的受力情况。
一、.浮力的四种计算方法:
F浮=F向上-F向下;
F浮=G-F拉;
F浮=G排=ρ液gV排;
F浮=G物(漂浮或悬浮)
二、.物体沉浮条件:
找准上浮、悬浮、下沉时,各自对应的F浮和G物的关系;
以及液体密度和物体密度的关系,V排和V物的关系
上浮的最后结果是漂浮(浮在液面上、静止在液面上)F浮=G物、ρ液>ρ物、V排<V物
悬浮(停留在液体中任何深度的地方、静止在液体中)F浮=G物、ρ液=ρ物,
V排=V物。
下沉的最后结果是沉底(停留在容器底部、静止在容器底部)F浮 F支=G物、
ρ液<ρ物、V排=V物。
三、隔离法.分析物体受力情况:(先重力再接触再摩擦)
首先把受力物体隔离出来
①先找不接触就可以产生的力重力,
②再找必须与受力物体接触才能产生的:支持力、压力、拉力、推力、浮力等
③最后判断物体是否受摩擦力的作用。
根据题目中,物体所处的静止或匀速直线运动状态(平衡状态) ,来求解未知力的大小和方向。
典型例题1:
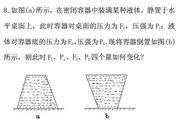
如图1所示,水平放置的平底柱形容器A内装一些水,不吸水的正方体物块B的边长10cm,用细线(重力和体积忽略不计)拉住物块B,细线的另一端固定在容器底部,静止后物块B浸入水中的体积为6×10⁻⁴m³,此时细线被拉直,长6cm,物块B所受拉力为1N,(水的密度1.0×10³kg/m³,g取10N/kg)。

图1
求:
(1)物块B受到的浮力
(2)物块B受到的重力
(3)水对容器底部的压强
解析:
(1)物块B排开水的体积,V排=6×10⁻⁴m³
根据阿基米德原理:F浮=G排=ρ水gV排=1.0×10³kg/m³x10N/kgx6×10⁻⁴m³=6N
(2)如图所示,物块B受到竖直向下的重力GB,竖直向下的拉力F拉=1N,还有竖直向上的浮力F浮=6N;并且物块B在这三个力的作用,处于静止状态;即三个力互为平衡力。
根据平衡力的知识:F浮=GB F拉
物块B受到的重力:GB=F浮--F拉=6N--1N=5N.。
(3)物块B的底面积S=10cmx10cm=100c㎡=10-2㎡
浸入水中的深度hB=V排/s=6×10⁻⁴m³/10⁻2㎡=0.06m
已知细绳被拉长时,细绳长L绳长=6cm=0.06m
容器底部水的深度h=L绳长 hB=0.06m 0.06m=0.12m
则水对容器底部的压强:P=p水gh=1.0×10³kg/m³x10N/kgx0.12m
=1.2×10³pa。
典型例题2:
如图2所示,向底面积为100c㎡的柱形容器中加水,再将一个质量为500g、体积为600cm³的木块用轻质细线拉住让其浸没在该容器的水中。求:
(1)细线对物块的拉力,
(2)剪断细线后,物体静止时浸入水中的体积。

图2
解析:
(1)木块浸没在水中,木块排开水的体积,V排=V木=600cm³=6×10⁻⁴m³
根据阿基米德原理:F浮=G排=ρ水gV排=1.0×10³kg/m³x10N/kgx6×10⁻⁴m³=6N
木块的质量: m木=500g=0.5kg,
根据公式G=mg, 木块重G木=m木g=0.5kgx10N/kg=5N,
木块受到竖直向下的重力G木=5N,竖直向下的拉力F拉,还有竖直向上的浮力F浮=6N;并且木块在这三个力的作用,处于静止状态;即三个力互为平衡力。
根据平衡力的知识:F浮=G木 F拉,
木块受到的拉力:F拉=F浮--G木=6N--5N=1N.。
(2)由于木块浸没在水中受到的浮力F浮=6N,大于木块的重力G木=5N,
即:F浮>G木,所以剪断细线后,木块上浮最后静止时漂浮在水面上。
根据物体漂浮在液面上的条件:F浮=G物
即木块漂浮在水上时所受到的浮力:F浮1=G木=5N
根据阿基米德原理:F浮1=ρ水gV排1
木块静止时浸入水中的体积:V浸=V排1=F浮1/ρ水g
=5N//1.0×10³kg/m³x10N/kg=5×10⁻⁴m³。
典型例题3
如图3所示,用细线悬挂的物体浸没在水中。已知水的深度为10cm,物体的体积为500cm³,薄壁柱形容器的底面积为100c㎡,细线对物体的拉力大小为4N。忽略容器重。
(水的密度1.0×10³kg/m³,g取10N/kg)。
求:
(1)物体的密度,
(2)水对容器底部的压力。
(3)剪断细线后容器对桌面的压强

图3
解析:
(1)由题意知,物体浸没在水中,
V排水=V物=500cm³
=5x10⁻⁴m³
物体所受到的浮力:
F浮=p水gV排
=1.0×10³kg/m³x10N/kgx5x10⁻⁴m³=5N。
由题意得,浸没在水中的物体受到三个力的作用:
即方向竖直向下的重力G物、竖直向上的浮力F浮和竖直向上的拉力F拉。
并且物体在这三个力的作用下,处于静止状态,三个力互为平衡力。
G物=F拉 F浮=4N 5N=9N
根据公式G物=m物g
物体的质量m物=G物/g
=9N/10N/kg=0.9kg
物体的密度:
p物=m物/V物=0.9kg/5x10⁻⁴m³
=1.8×10³kg/m³。
(2)容器中水的深度;h=10cm=0.1m
水对容器底部的压强:
P=p水gh
=1.0×10³kg/m³x10N/kg
x0.1m=1000pa。
典型例题4:
如图4甲所示,一个底面积为400c㎡的薄壁圆柱形容器置于水平地面上,装有0.3m深的水。现将物体A放入其中,物体A漂浮于水面上,如图乙所示,此时容器底部受到水的压强比图甲增大了400Pa。当再给物体A施加一个竖直向下大小为4N的力F以后,物体A恰好浸没水中静止(水未溢出),如图丙所示。
(p水=1.0×10³kg/m³, g 取10 N/kg)
求:

图4
(1)容器中水的质量。
(2)物体A放入前,容器底部受到水的压强。
(3)物体A的密度。
解析:
(1)容器中水的体积:
V水=Sh=0.04㎡×0.3m
=1.2×10-2m³,
容器中水的质量:
m水=p水V水
=1.0x10³kg/m³x1.2x10¯2 m³=12 kg.
(2)物体A放入前,容器底部受到水的压强:
P水=p水gh=1x10³ kg/m³x10N/kgx0.3m
=3x10³ Pa.
(3)物体A漂浮与放入前,水对容器底增大的压强△P1=400 Pa,
由p=pgh 得,水面上升的高度:
△h1=△P1/p水g
=400pa/1.0×10³kg/m³x10N/kg=0.04m。
则,物体漂浮时排开水的体积:V排1=S△h1
=0.04m2x0.04m
=1.6X10—3m³。
根据阿基米德原理公式:
F浮1=p水gV排1
=1.0×10³kg/m³x10N/kg
x1.6x10⁻3m³=16N。
由于物体漂浮在水面上,
GA=F浮1=16N,
根据G=mg
物体A的质量为:
mA=GA/g=16N/10N/Kg
=1.6kg。
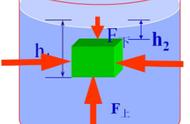
物体A浸没后,受到三个力的作用:方向竖直向下的重力GA=16N和压力F=4N,
还有方向竖直向上的浮力
F浮2,如图5所示:

物体A在GA、F和F浮2的作用下处于平衡状态(静止),所以三个力互为平衡力。
F浮2=GA F=16N 4N=20N
根据阿基米德原理:
F浮2=p水gV排2
浸没时:
VA=V排2=F浮2/p水g
=20N/1.0×10³kg/m³
x10N/kg=2x10-3m³
则物体的密度:
pA=mA/VA
=1.6kg/2x10-3m³
=0.8×10³kg/m³。
,