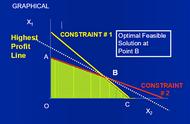
随手翻开以前的高考试卷,看到一道线性规划题,于是拿出高中数学必修五,复习一下线性规划的知识。
线性规划的主要概念有两个:一是判断二元一次不等式所表示的区域;二是求目标函数的最优解。它们都涉及判断方向。
判断二元一次不等式所表示的区域在直线的哪边,教材是取点判断,看了几本教辅,也是说“线定界,点定域”。直线不经过原点,取原点判断;直线经过原点,取其他特殊点判断。感觉这种方法不太好。
我的判断方法是,用x、y的方向判断。比如判断不等式2x-y-4≤0的平面区域,正变量小负变量大即可,即x小y大,为直线的左上区域。
总结就是:不等式是大于零,正变量大负变量小;不等式是小于零,正变量小负变量大。根据这个原理来判断平面区域的方向。左上、右上、左下、右下。
其实我们判断x>2的区域,也不是取点判断,而是根据变量的方向判断。同理,我们判断x y-1≥0,也可以根据变量的方向判断,正变量大负变量小,即x大y大,在直线的右上方。
求目标函数的最优解也可以同理判断方向。比如求z=2x y的最优解,显然x大y大为最大值方向,向右上平移到可行域的最远顶点,就是最大值。最小值相反。
而教材必修五求目标函数的最优解的根据是,目标函数的最大值与最小值总是在区域边界交点处取得,如有四个交点,它全算出来,然后比较大小。显然没有必要。
教材没写好,教辅跟着绕弯,学生浪费精力,没有学到最好的方法。
高考线性规划题大约有五分,可以秒*。
教材太老了,需要改一改。
学习很容易,看你会不会。
用最简方法,学最难数学。