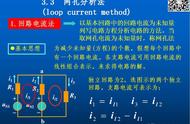
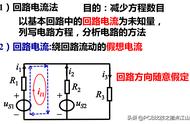
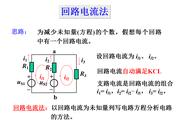
支路电流法,对于中职阶段的学生而言是一种必须要掌握的用于求解复杂电路的的基本办法之一。下面我们从以下几个方面来对其进行分析:
第一点: 基本知识 基尔霍夫定律
基尔霍夫定律分为KCL(电流)与KVL(电压)两部分,其内容如下:
KCL:对于电路中的任意一个节点(包括闭合回路),任意时刻,流入节点的电流之和总是等于流出节点的电流之和。
KVL:对于电路中的任意一个回路,从回路上任意一点出发,沿回路绕行一周,则各段电压的代数和为0。
注意: 对于KVL,采用以上定义时,绕行过程中所遇到的电源电动势当做电压对待,这里的对待,指的是其方向即由高电位指向低电位。
第二点: 明确方程组的方程数及其类别
对于具有b条支路,n个节点的复杂电路,我们采用支路电流法求解时,一共需要列写b个方程,其中电流方程的数目为n-1个,剩余的b-(n-1)个方程均为KVL电压方程。
第三点:解题步骤
1.观察电路图,并假设各支路电流的参考方向(利用KCL列电流方程),假设回路的绕行方向(利用KVL列电压方程,一般选择网孔作为计算回路)
注意:假设的方向需要在电路图上标示出来,作为解题的支撑依据
2.列写方程组,对于节点采用KCL,流入节点的电流等于流出节点的电流。对于回路采用KVL,绕行回路一周各段电压代数和为0(求解代数和时,将各段电压方向与回路绕行的方向做对比,若同向则电压取正值,反之则为负值)
注意:有电流流过电阻,则电阻两端就有电压,其电压方向与流经电阻的电流方向相同。
3.代入已知量,求解方程组,若结果为负值,则表明该电流实际方向与假设的参考方向相反,若为正值,则方向相同。
总之,支路电流法,其本质即为对基尔霍夫定律的实际应用。