边界值分析法定义在边界外的点,边界值分析法总结心得

边界值分析法是一种很实用的黑盒测试用例方法，它具有很强的发现故障的能力。边界值分析法也是作为对等价类划分法的补充，测试用例来自等价类的边界。

这个方法其实是在测试实践当中发现，Bug 往往出现在定义域或值域的边界上，而不是在其内部。为检测边界附近的处理专门设计测试用例，通常都会取得很好的测试效果。

在用边界值分析法的时候，一般规定了取值范围以及值的个数的场景。

在分析等价类案例，划分等价类的时候，一般都是会有比较特殊的点，叫做极点或者上点。比如 [1,100] 中的上点就是 1 和 100，这两个数值就被称为边界值，也可以叫极值。设计测试用例的时候，可以在等价类的基础上，去重点验证它的边界点的情况。

比如需求中的要求是输入的参数值必须大于等于 0 同时小于 100 的整数。

正确代码可以这样设置判断条件：

# 正确条件 1 num > -1 and num < 100 # 正确条件 2 num >= 0 and num <= 99

但是在实际的代码编写过程中，很有可能因为各种原因，导致判断条件设置错误：

# 错误条件 1 num >= -1 and num <= 101 # 错误条件 2 num > 0 and num < 101 # 错误条件 3 num >= 1 and num <= 100

第一种错误情况是因为多包含了 -1 和 101，第二种错误情况是或者漏掉了 0，而第三种错误情况是漏掉了 0 并且多包含了 100。

因为会有各种错误情况的出现，所以需要选择边界值进行重点测试来避免这些情况。

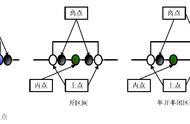
使用边界值分析法设计用例需要考虑 3 个点的选择。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-N0Djr1p6-1661957017336)(upload://nNwjLMu9tmnZPu3eZAUkXyq9rbx.png)]

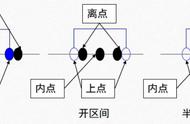
• 上点：边界上的点
• 离点：离上点最近的点。如果输入域是封闭的，则离点在域范围外；如果输入域是开区间，则离点在域的范围内。
• 内点：在输入域内任意一个点

要选取正好等于、刚好大于或刚好小于边界值作为测试数据，一般来说要把上点、离点和内点都取到。所以选取正好等于、刚好大于或刚好小于边界值作为测试数据。

综上，题目中要选择的点有六个：正好等于边界值的 0、100，刚好小于边界值的 -1、99，刚好大于边界值的 1、101。

1. 如果规定了输入域的取值范围，则选取刚好在范围边界的点，以及刚好超过边界的点，作为测试的输入数据。
2. 如果规定了输入值的个数，则用最大个数，最小个数，比最小个数少 1，比最大个数多 1 的数作为测试数据。
3. 如果规定了输入是一个有序的集合，则选取集合的第一个元素和最后一个元素作为测试数据。

问题：计算 1—100 的整数之和（包括 1 和 100）

上面已经用等价类的方法设计出来的测试用例，现在要使用边界值分析法补充用例。

首先分析边界值：1，100（有效等价类），其次是边界值两边的值：0，2，99，101（0 和 101 是无效等价类，2 和 99 是有效等价类）。

把有效等价类中的数值换为边界值，这里有 4 个有效等价类的值要取，分别是 1，2，99，100，那么这四个值两个输入框都需要取到。无效等价类中也要覆盖到 0 和 101 这两个值，同样的两个输入框都需要覆盖。

用边界值法补充测试用例时，要注意确定边界情况（输入或输出等价类的边界），选取正好等于、刚刚好大于或刚刚好小于边界值作为测试数据以及确定各个值的等价类，明确边界值和等价类区别，即边界值分析不是从某等价类中随便挑一个作为代表，而是这个等价类的每个边界都要作为测试条件。

[更多技术文章](https://qrcode.ceba.ceshiren.com/link?name=article&project_id=qrcode&from=toutiao×tamp=1662397200&author=Muller)