有段时间没有写了,觉得很有必要继续加油写下去。一直有想梳理下主要的机器学习算法了,做一个从各个主流算法到新兴的算法,都做一番回顾,理论结合代码实践,做一个复习,毕竟温故而知新。顺便说下,什么机器学习,数据挖掘,人工智能,这几个词语很多,也很容易用的模糊了,边界不是很清晰,我也不想做过多的解读与区分,免得弄巧成拙,或者班门弄斧,还是埋头实践吧。
后面的几篇主要从这么几个类别来整理:
分类算法;
聚类算法;
关联算法;
其他算法;
这么我们以一个就来个经典的分类算法,神经网络算法。(以下摘自本人的毕业设计论文,部分公式用图片代替,由于公式很难编辑)
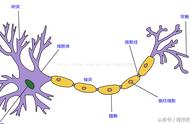
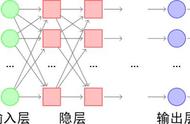
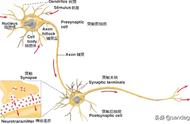
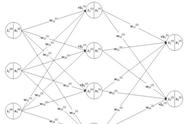
人工神经网络模型大多为BP网络(Back Propagation Network,BP),即反向传播学习算法[14、30]。它通常是由三层相同的一系列神经元构成的层状网络,底层为输入层,中间为隐含层,顶层为输出层,如图2.2。信号在相邻各层间逐层传递,不相邻的各层间无联系。神经网络方法的优点是应用方便,获得结果较快较好;主要的缺点是利用了大量的可调参数,使结果不易解释和理解。
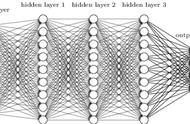
BPN是一种单向传播的多层前向神经网络,其结构为除输入输出结点外,有一层或多层隐含结点,同层结点间无任何联接,由于同层结点上无任何耦合,故每层结点的输出只影响下一层结点的输出。因此,可将BP网络看作从输入到输出的一种高度非线性映射,它也是目前应用最广泛的一种模型。BP算法是在导师指导下,适合于多层神经元网络的一种学习模型,它是建立在梯度下降法基础上的[30]。

图2.2 人工神经网络示意图
算法描述:

(2.2.1)
若和E都小于允许的误差,则学习过程结束,否则计算各层节点的输出偏差,进行误差反向传播,修改网络连接权值和阈值。


网络连接权值和节点阈值,经过上述过程的反复修正,逐渐趋于稳定的值。
采用BPN法的过程中需要选择的几个参数
①学习率和惯性因子
BP算法本质上是优化计算中的梯度下降法,利用误差对于权、阀值的一阶导数信息来指导下一步的权值调整方向,以求最终得到误差最小。为了保证算法的收敛性,学习率必须小于某一上限,一般取0<<1而且越接近极小值,由于梯度变化值逐渐趋于零,算法的收敛就越来越慢。在网络参数中,学习率和惯性因子是很重要的,它们的取值直接影响到网络的性能,主要是收敛速度。为提高学习速度,应采用大的。但太大却可能导致在稳定点附近振荡,乃至不收敛。针对具体的网络结构模型和学习样本,都存在一个最佳的学习率和惯性因子,它们的取值范围一般0~1之间,视实际情况而定。
②初始权值和阈值
在前馈多层神经网络的BP算法中,初始权、阈值一般是在一个固定范围内按均匀分布随机产生的。一般认为初始权值范围为-1~+1之间,初始权值的选择对于局部极小点的防止和网络收敛速度的提高均有一定程度的影响,如果初始权值范围选择不当,学习过程一开始就可能进入“假饱和”现象,甚至进入局部极小点,网络根本不收敛。初始权、阈值的选择因具体的网络结构模式和训练样本不同而有所差别,一般应视实际情况而定。
③收敛误差界值Emin
在网络训练过程中应根据实际情况预先确定误差界值。误差界值的选择完全根据网络模型的收敛速度大小和具体样本的学习精度来确定。当Emin值选择较小时,学习效果好,但收敛速度慢,训练次数增加。如果Emin值取得较大时则相反。
参考文献:
[14] 樊龙江,生物信息学札记, 浙江大学生物信息学研究所,2005.04,87-90
[30] 焦李成,神经网络系统理论,西安:西安电子科技大学出版社,1995