数学常数是与数学相关的固定数值,它们在数学中起着非常重要的作用。这些数值通常是通过各种方式推导出来的,包括数学理论、实验观测、数值模拟等等。以下是一些可能产生数学常数的方式:
- 数学推导:数学家们通过研究各种数学对象和结构,发现了很多固定的数值。这些数值通常是由各种公式、方程或等式导出的,例如圆周率、自然对数的底数等。
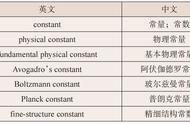
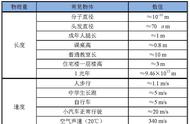
- 实验观测:在物理学、化学、天文学等领域,科学家们经常需要测量和观测各种物理量。在这些观测过程中,可能会出现一些固定的数值,例如普朗克常数、光速等。
- 数值模拟:在一些复杂的计算中,可能需要进行数值模拟来近似解决问题。在这个过程中,会出现一些固定的数值,例如计算机中的机器精度等。
- 自然现象:在自然界中,有一些现象具有固定的数值,例如电荷量、引力常数等。这些数值可能影响到数学中的各种问题,从而成为数学常数。
总之,数学常数可以通过各种途径产生,它们在数学和其他科学领域中具有广泛的应用。
二、以人名命名的常数、分布、函数、方法这些以人名命名的常数、分布、函数、方法等,代表了各个时期的科学巨匠的杰出贡献,为各个领域的研究提供了重要的工具和思想。
以下是数学中以人名命名的一些常数:
- 欧拉数(Euler's number):也称为自然对数的底数,通常用字母e表示。它以瑞士数学家欧拉(Leonhard Euler)的名字命名,是数学中的一个重要常数,它在微积分、概率论、统计学、物理学等领域都有广泛的应用。
- 美因数(Mersenne's number):指形如2^n-1的自然数,其中n是一个自然数。它以法国数学家美因(Marin Mersenne)的名字命名,是一个重要的数学研究对象,与梅森素数密切相关。
- 黄金比例(Golden Ratio):也称为黄金分割或黄金分界点,通常用希腊字母φ表示。它以古希腊数学家菲迪亚斯(Phidias)的名字命名,是一种特殊的比例关系,具有美学上的价值,也在几何学、艺术等领域有广泛的应用。
- 阿克曼常数(Ackermann constant):指阿克曼函数的常数项,通常用字母A表示。它以德国数学家威尔海姆·阿克曼(Wilhelm Ackermann)的名字命名,是计算机科学中的一个重要常数,与计算机算法的复杂性密切相关。
- 莱布尼兹公式中的莱布尼兹(Leibniz):莱布尼兹公式是计算π的一种方法,其中的莱布尼兹指德国数学家莱布尼兹,他在17世纪提出了这个公式。
- 斯特林数(Stirling numbers):指将n个元素划分成k个非空子集的方案数,通常用字母S表示。它以苏格兰数学家詹姆斯·斯特林(James Stirling)的名字命名,是组合数学中的一种数列,具有重要的组合意义和应用。
- 卡拉扬常数(Karatsuba constant):指两个n位整数相乘的基本操作次数,通常用字母K表示。它以俄罗斯数学家安德烈·卡拉茨巴(Andrey Karatsuba)的名字命名,是计算机科学中的一个重要常数,与算法的时间复杂度密切相关。
- 狄利克雷常数(Dirichlet's constant):指调和级数与素数密度之比的常数,通常用字母D表示。它以德国数学家彼得·狄利克雷(Peter Gustav Lejeune Dirichlet)的名字命名,是数论中的一个重要常数,与素数分布、调和级数等问题相关。
- 波利亚常数(Pólya constant):指正方形网格上最长的不重叠的棋盘多边形的周长与边数的比值,通常用字母λ表示。它以匈牙利数学家波利亚(George Pólya)的名字命名,是组合几何中的一个重要常数,与计数问题、对称性问题等密切相关。
- 约瑟夫斯问题中的约瑟夫斯(Josephus):约瑟夫斯问题是一个经典的数学游戏问题,其中的约瑟夫斯指古罗马历史学家弗拉维约瑟夫斯(Flavius Josephus),他据说在犹太人叛乱中幸存下来,因而成为了这个问题的著名人物。
- 索洛维亚定理中的索洛维亚(Sylvester):索洛维亚定理是关于数学彩虹问题(Rainbow Problem)的一个定理,其中的索洛维亚指英国数学家詹姆斯·约瑟夫·索洛维亚(James Joseph Sylvester),他是19世纪英国数学界的杰出人物之一。
- 埃尔米特多项式(Hermite polynomials):指由法国数学家查尔斯·埃尔米特(Charles Hermite)引入的一类特殊的正交多项式,具有广泛的应用。
- 伯努利数(Bernoulli numbers):指由瑞士数学家雅各布·伯努利(Jacob Bernoulli)和他的侄子约翰·伯努利(Johann Bernoulli)研究的一类数列,具有广泛的应用,如在数论、组合数学、微积分等领域中。
- 卡普雷卡数(Kaprekar constant):指将任意四位数的所有数字重新排列后,得到的最大数和最小数之差,重复这个过程直到最终结果不再变化,得到的常数。它以印度数学家德鲁维·卡普雷卡(D. R. Kaprekar)的名字命名。
- 斐波那契数列(Fibonacci sequence):指由意大利数学家列奥纳多·斐波那契(Leonardo Fibonacci)在13世纪初提出的一个数列,其中每个数都是前两个数之和,具有广泛的应用,如在金融、自然科学、艺术等领域中。
- 卡塔兰数(Catalan numbers):指由比利时数学家欧仁·查理·卡塔兰(Eugène Charles Catalan)在19世纪提出的一类数列,具有广泛的应用,如在组合数学、几何学、代数学等领域中。
- 柯西序列(Cauchy sequence):指由法国数学家奥古斯丁·路易·柯西(Augustin-Louis Cauchy)在19世纪提出的一类数列,具有重要的数学性质,如完备性、连续性等。
- 傅里叶级数(Fourier series):指由法国数学家让·巴蒂斯特·约瑟夫·傅里叶(Jean-Baptiste Joseph Fourier)在19世纪提出的一类级数,可以将任意周期函数表示为正弦函数和余弦函数的线性组合,具有广泛的应用,如在物理学、工程学、信号处理等领域中。
- 基尔霍夫定律(Kirchhoff's laws):指德国物理学家叶夫根·基尔霍夫(Gustav Kirchhoff)在19世纪提出的两条物理定律,描述了电路中电流和电势的分布关系,具有重要的应用。
- 欧拉数(Euler numbers):指由瑞士数学家欧拉(Leonhard Euler)研究的一类数列,具有广泛的应用,如在代数学、组合数学、微积分等领域中。
- 雅可比矩阵(Jacobi matrix):指由德国数学家卡尔·雅可比(Carl Gustav Jacob Jacobi)在19世纪提出的一类矩阵,描述了一类特殊的线性变换,具有广泛的应用,如在量子力学、微分几何学、数学物理等领域中。
- 雅可比-福克矩阵(Jacobi–Fock matrix):指由德国数学家卡尔·雅可比和俄国数学家弗拉基米尔·福克(Vladimir Fock)研究的一类矩阵,描述了量子力学中的多体系统,具有重要的应用。
- 拉格朗日乘数(Lagrange multiplier):指由意大利数学家约瑟夫·路易斯·拉格朗日(Joseph-Louis Lagrange)在18世纪提出的一种优化方法,用于求解约束条件下的极值问题,具有广泛的应用,如在经济学、物理学、工程学等领域中。
- 莫比乌斯函数(Möbius function):指由德国数学家阿道夫·莫比乌斯(August Ferdinand Möbius)研究的一种函数,用于描述数论中的一类重要性质,如素数分布、数论函数的互反关系等。
- 帕累托分布(Pareto distribution):指由意大利经济学家维尔弗雷多·帕累托(Vilfredo Pareto)在19世纪末提出的一种概率分布,描述了极端事件的出现概率,具有广泛的应用,如在经济学、金融学、生态学等领域中。
- 柏松分布(Poisson distribution):指由法国数学家西蒙·柏松(Siméon Denis Poisson)在19世纪研究的一种概率分布,描述了在一个固定时间内,一个随机事件发生的次数,具有广泛的应用,如在物理学、生物学、金融学等领域中。
- 普朗克常数(Planck constant):指由德国物理学家马克斯·普朗克(Max Planck)在20世纪初提出的一个物理常数,用于描述微观世界中粒子的能量和频率之间的关系,是量子力学理论的基础,具有重要的应用。
- 拉格朗日插值法(Lagrange interpolation):指由意大利数学家约瑟夫·路易斯·拉格朗日(Joseph-Louis Lagrange)在18世纪提出的一种多项式插值方法,用于在一组已知数据点的基础上,求解多项式函数,具有广泛的应用,如在计算机图形学、信号处理、金融工程等领域中。
- 伯努利数(Bernoulli number):指由瑞士数学家雅各布·伯努利(Jacob Bernoulli)和他的侄子约翰·伯努利(Johann Bernoulli)研究的一类数列,用于描述数学中的一些重要问题,如无穷级数求和、特殊函数定义等。
- 斯特林数(Stirling number):指由苏格兰数学家詹姆斯·斯特林(James Stirling)研究的一类数列,用于描述组合数学中的一些问题,如集合划分、多项式展开等。
- 罗斯福数(Rosenhain number):指由德国数学家费迪南德·罗森哈因(Ferdinand Rosenhain)研究的一类二次代数曲线,用于描述平面几何中的一些问题,如椭圆曲线加密算法中的离散对数问题。
- 拉姆努金常数(Ramanujan constant):指由印度数学家斯里尼瓦瑟·拉马努金(Srinivasa Ramanujan)提出的一类数学常数,具有神秘而美妙的性质,如与圆周率的关系、与自然对数的关系等。
- 卡方分布(Chi-squared distribution):指由英国统计学家卡尔·皮尔逊(Karl Pearson)研究的一种概率分布,用于描述样本数据与理论模型之间的偏离程度,具有广泛的应用,如在假设检验、回归分析等领域中。
- 拉普拉斯变换(Laplace transform):指由法国数学家皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)研究的一种数学变换,用于将一个时间域上的函数,转换为一个复频域上的函数,具有在控制论、信号处理、电路分析等领域中的应用。
- 维纳过程(Wiener process):指由美国数学家诺伯特·维纳(Norbert Wiener)在20世纪初提出的一种随机过程,用于描述随机漫步、布朗运动等现象,具有在金融工程、物理学、生物学等领域中的应用。