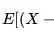从本质上讲,协方差和相关性都是衡量两个变量之间关系和依赖关系的工具。根据他们的定义,协方差表示两个变量之间线性关系的方向方面,而相关性是这种线性关系的强度和方向的度量。从更广泛的角度来看,相关性可以看作是协方差的派生函数。让我们详细讨论这两个术语。
协方差:协方差是一个统计术语,指的是两个随机变量之间的系统关系,其中另一个变量的变化反映了一个变量的变化。它的范围可以从 -∞ 到 ∞,负值表示负关系,正值表示正关系。
这个数字越大,关系的依赖性就越强。正数或正协方差表示直接关系。相反,负值表示负协方差,表示两个变量之间的负相关。虽然协方差在表征关系类型时很有用。
要计算协方差,可以使用以下公式,考虑由变量 x 和 y 表示的两组数据点:

- ˉ x ˉ 和 ˉ y ˉ 是变量x和y的均值,
- n 是数据点的数量。
在 Python 中使用 NumPy,可以使用cov()方法方便地计算协方差。下面是一个示例:
import numpy as np
# Sample data for two variables
variable1 = np.array([1, 2, 3, 4, 5])
variable2 = np.array([5, 4, 3, 2, 1])
# Calculate covariance
print(np.cov(variable1, variable2))
生成的协方差矩阵
Covariance matrix=
[cov(variable1,variable1 )cov(variable2,variable1)
cov(variable1,variable2)cov(variable2,variable2)]
- 对角线元素表示变量 1 和变量 2 的方差(正协方差)。
- 非对角线元素表示变量 1 和变量 2 之间的协方差,反之亦然(负协方差)。
在提供的示例中,输出矩阵 [[2.5, -2.5], [-2.5, 2.5]] 表示变量 1 和自身的正协方差,变量 2 和自身的正协方差,以及变量 1 和变量 2 之间的负协方差。
现在,通过考虑变量 1 和变量 2 之间的协方差来解释这个矩阵:
- 值为-2.5,表示协方差为负。平均而言,变量 1 每更改一个单位,变量 2 往往会减少 2.5 个单位。这表明存在反比关系:随着变量 1 的增加,变量 2 通常会减小。
- 相反,变量 2 中每变化一个单位,变量 1 往往会减少 2.5 个单位。这强化了反比关系,说明随着变量 2 的增加,变量 1 趋于减小。
总之,负协方差突出了变量 1 和变量 2 之间的负相关关系,为了解它们关系的方向和强度提供了有价值的见解。
相关:相关性是一种统计度量,用于量化两个随机变量之间线性关系的强度和方向。与协方差不同,协方差不是标准化的,可以取任何实际值,相关性是归一化的,并且始终在 -1 到 1 的范围内。
- 相关性为 1 表示完全正线性关系:当一个变量增加时,另一个变量也线性增加。
- 相关性为 -1 表示完美的负线性关系:当一个变量增加时,另一个变量线性减小。
- 相关性为 0 表示变量之间没有线性关系。
为了计算相关性,可以使用以下公式,考虑由变量 x 和 y 表示的两组数据点:

- σ(x) 和 σ(y) 分别是 x 和 y 的标准差。
在 Python 中,使用 NumPy,可以使用corrcoef()该方法计算相关性。下面是一个示例:
import numpy as np
# Sample data for two variables
variable1 = np.array([1, 2, 3, 4, 5])
variable2 = np.array([5, 4, 3, 2, 1])
# Calculate correlation coefficient
print(np.corrcoef(variable1, variable2))
生成的协方差矩阵提供了对两个变量的联合相关性的见解:
Correlation matrix=
[corrcoef(variable1,variable1) corrcoef(variable2,variable1)
corrcoef(variable1,variable2) corrcoef(variable2,variable2)]
解释输出:
- 对角线元素表示变量 1 和变量 2 的相关性
- 非对角线元素表示变量 1 和变量 2 之间的相关性,反之亦然。
在提供的示例中,输出矩阵 [[1. -1.], [-1.1.]] 表示变量 1 和变量 2 的相关结构。
现在,通过考虑变量 1 和变量 2 之间的相关性来解释这个矩阵:
- 该值为 -1,表示完全负相关。这意味着随着变量 1 的增加,变量 2 始终以线性方式减少。
- 相反,变量 2 每增加一个单位,变量 1 往往会持续减少 1 个单位。这加强了完美的负相关,说明随着变量 2 的增加,变量 1 趋于线性减小。
总之,-1 的相关系数突出了变量 1 和变量 2 之间的强负相关关系,为了解其线性关系的方向和强度提供了有价值的见解。
总之,对协方差和相关性的探索揭示了变量之间的关系。协方差为我们提供了这种关系的方向性感觉,而相关性(一种标准化的度量)提供了更清晰的比较。
,