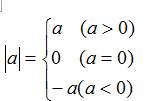欢迎关注:“黔中初数张文松”!

绝对值是初中数学的一个重要的内容。同时也是很多同学学习上的一个难点。为突破这个难点,本文为你分享一篇“漫话绝对值”的文章。从中你可以更好的认识、理解和掌握绝对值这个知识点。
大家好!我叫绝对值。我是初中数学中的一个不可缺少的而且相当重要的角色。许多同学在学习之中,正因为没有真正的认识我,所以,很多地方栽了跟斗!
我是数的一个重要组成部分(任何一个非0的数都是由符号和我两部分组成),七年级的新同学要注意啦,数的范围扩充到有理数以后,每一个数,无论是运算中的数还是运算结果中的数,你都要考虑这个数的符号是什么?绝对值是什么?缺一不可哦!养成一个认识和表达一个数的好习惯。因此,提到数必然少不了我。那,我到底是什么?长什么样?且听我慢慢为你道来:
首先,你可以通过数轴来认识我,因为数轴是我的好伙伴。“数轴上,表示一个数a的点到原点的距离就叫做a的绝对值”。因此,可以说我就是距离。距离可以为0,但是距离不能为负(因为距离只有远近)。所以,我是一个非负数。我的长相是在一个数的两侧各加一根短竖线。"|*|"这身装扮还时髦吧?比如"|a|"这就是a的绝对值,"|-5|"这就是的-5绝对值,"|π-3.14|"这就是π-3.14的绝对值,等等。
第二,不同类型的数中,我与原数的关系是不一样的。“正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值是0”.有的同学,就在这里没有很好的认识我。那怎样理解我和正数、负数和0这三类数之间的关系呢?以及怎样根据这几种关系来计算(或化简)一个数的绝对值呢?做到两个方面:
1.能把上面的关系翻译成符号语言(当然课本已经给你翻译好的,但是你要理解它):
(1)若a>0(意为a是正数),则|a|=a;
(2)若a=0,则|a|=0;
(3)若a<0(意为a负数),则|a|=-a;
把这些符号语言再变一种形式:

通俗地说,要计算(或化简)一个数的绝对值,首先得看我的时装“| |”里包裹的是什么数。如果是正数,直接脱掉我的时装“| |”即可;如果是0,也同样脱掉时装“| |”;如果是负数,脱掉时装“| |”的同时,还要添上一个负号“-”。因此,当我穿着时装出现的时候,你要为我减负,让我轻装上阵时,你得首先判断时装里的数是什么数。不能随意脱下我的时装,否则,你要受到惩罚的!
2.将上面的关系反过来看看:
(1)绝对值等于它本身的数是正数?
(2)绝对值等于0的数是0?
(3)绝对值等于它的相反数的数是负数?
或者,将符号语言反过来,
(1)若|a|=a,则a>0?
(2)若|a|=0,则a=0?
(3)若|a|=a,则a<0?
结论:绝对值等于它本身的数是非负数(不仅是正数,还有0);绝对值等于它的相反数的数是非正数(不仅是负数,还有0)。翻译过来是:若|a|=a,则a≥0(多了一个等号哦!)若|a|=-a,则a≤0(也多了一个等号)。
第三,你知道我会以哪些形式出现在考题中呢?主要有三种:
1.计算,如:
(1)|-3|=______;(2)|π-3.14|=_______.
答案:(1)3;(2)π-3.14.
2.化简,如:
(1)当m>2时,化简|2-m|=_________;
(2)若n/m<0,化简|mn|=__________.
答案:(1)m-2;(2)-mn.
3.求字母的取值范围
(1)若|2a-1|=1-2a,则a的取值范围是_____________;
(2)若|a-b|=a-b,则a、b的关系是_______________.
答案:(1)a≤1/2;(2)a≥b.
这就是我!不管你喜不喜欢我,要学好数学,你必须懂我!
感谢关注!欢迎留言!欢迎评论!
,