等式转换
通过多次的等式转换。终于可以将这两个等式进行合并了!如下:

最终等式转换
这个等式成立有一个前提!就是关于模反元素的,就是当整数e和φ(n)互质!一定有一个整数d是e相对于φ(n)的模反元素。
我们可以测试一下。
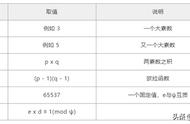
m取值为4
n取值为15
φ(n)取值为8
e 如果取值为3
d 可以为 11、19...(模反元素很明显不止一个,其实就是解二元一次方程)
如果你测试了,那么你可以改变m的值试一下,其实这个等式不需要m和n 互质。只要m小于n 等式依然成立。
这里需要注意的是,我们可以看做 m 通过一系列运算得到结果仍然是 m。这一系列运算中,分别出现了多个参数n、φ(n)、e还有d。
m 的 e乘上d 次方为加密运算,得到结果 c
c 模以 n 为解密运算,得到结果 m
这似乎可以用于加密和解密。但这样,加密的结果会非常大。明文数据将非常小(虽然RSA用于加密的数据也很小,但是没这么大悬殊),真正的RSA要更加强大,那么RSA是怎么演变来的呢??
早期很多数学家也停留在了这一步!直到1967年迪菲赫尔曼密钥交换打破了僵局!
迪菲赫尔曼密钥交换这个密钥交换当时轰动了整个数学界!而且对人类密码学的发展非常重要,因为这个伟大的算法能够拆分刚才的等式。当非对称加密算法没有出现以前,人类都是用的对称加密。所以密钥的传递,就必须要非常小心。
迪菲赫尔曼密钥交换 就是解决了密钥传递的保密性,我们来看一下

迪菲赫尔曼密钥交换
假设一个传递密钥的场景。算法就是用3 的次方去模以17。 三个角色
- 服务器 随机数 15
- 这个15只有服务器才知道。通过算法得到结果 6 因为 3的15次方 mod 17 = 6 。然后将结果 6 公开发送出去,拿到客户端的 12 ,然后用12^15 mod 17 得到结果10(10就是交换得到的密钥)
- 客户端 随机数13
- 客户端用3 的 13次方 mod 17 = 12 然后将得到的结果12公布出去。
- 拿到服务器的 6 ,然后用6^13 mod 17 得到结果10(10就是交换得到的密钥)
- 第三者
- 第三者只能拿到6 和 12 ,因为没有私密数据13、15,所以它没法得到结果10。
为什么 6的13次方会和12的15次方得到一样的结果呢?因为这就是规律,我们可以用小一点的数字测试一下3^3 mod 17 = 10和10 ^ 2 mod 17 ; 3 ^ 2 mod 17 = 9和9^3 mod 17结果都是15。迪菲赫尔曼密钥交换最核心的地方就在于这个规律

迪菲赫尔曼密钥交换转换
RSA的诞生