加密——RSA前端与后台的加密与解密
什么是RSA加密
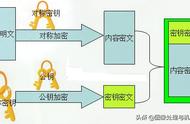
RSA加密算法是一种非对称加密算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密,则需要肜另一个才能解密,利用对极大整数做因数分解的难度决定了RSA算法的可靠性
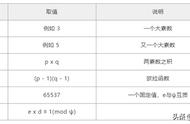
RSA的算法涉及三个参数,n、e1、e2
其中,n是两个大质数 p、q的积,n的二进制表示所占用的位数,就是所谓的密钥长度
e1和e2是一对相关的值,e1可以任意取,但要求与(p-1) * (q-1)互质;再选择e2,要求(e2 * e1) = 1 (mod(p-1) * (q-1))
(n,e1),(n,e2)就是密钥对,其中(n,e1)为公钥,(n,e2为公钥)
RSA加密解密算法完全相同,设A为明文,B为密文,则:A = B ^ e2 (mod n) ;B = A ^ e1 (mod n)
e2和e1可以互换使用,即:
A = B ^ e1 (mod n); B = A ^ e2 (mod n)
RSA流程
1.后端生成publicKey与privateKey
2.后端返回publicKey给前端
3.前台使用publicKey给敏感字段加密
4.使用post方式发送数据给后端
5.后端使用publicKey与pvivateKey进行解密。
使用加密库cryptico为数据加密
1.需要加密时先请求后台的getrsa接口,后台会返回加密公钥

2.定义加密方法

3.为数据加密