rsa的加密和解密原理,rsa算法的加密和解密步骤

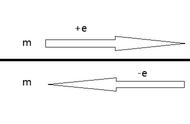
数据信息安全对我们每个人都有很重要的意义，特别是一些敏感信息，可能一些类似于收货地址、手机号还没引起大家的注意。但是最直白的，银行卡、姓名、手机号、身份证号，如果这些信息被黑客拦截到，他就可以伪装成你，把你的钱都取走。那我们该怎么防止这样的事情发生？报文加密解密，加签验签。

我害怕什么

我害怕卡里的钱被别人取走

我害怕转账的时候，报文被黑客拦截到，篡改信息转到别人的账户。

我害怕我的敏感信息被有心人获取

做一笔游戏充值，半个小时就收到各种游戏广告，我并不能抵挡诱惑

我要做什么

1. 交易报文不被篡改防止报文被篡改，需要对报文进行验签操作。
2. 敏感信息不被读取防止报文被读取，则需要将敏感信息加密。

公钥和私钥

公钥和私钥，加密解密和加签验签。加解密用来保证数据安全，加签验签用来证明身份。

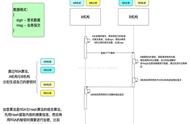
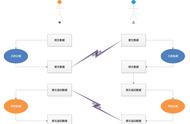
商户生成一对公私钥(商公，商私)，商户会把公钥给银行；银行也会生成一对公私钥(银公，银私)，银行会把公钥给商户。也就是说：商户有银行的公钥，自己的公钥和私钥。银行有商户的公钥，自己的公钥和私钥

• 加密解密保证数据安全：商户使用自己公钥加密，银行没有商户私钥解不开报文，排除商户使用自己的私钥加密，银行使用商户公钥解密。理论上可行，然而会出现这种情况，商户和银行1，2，3都使用相同的公私钥，那么自己私钥加密后发送给银行1的报文，被银行2截取到也可以被解密开，违背了我们加密的目的--保证数据安全，排除。商户使用银行的公钥加密，让银行用自己的私钥解密。理论上可行，然而会出现这种情况，银行会和商户A，B，C都使用相同的公私钥，那么商户A和商户B发送过去的报文，银行都能解开，而且只有此银行的私钥可以解开，达成了我们的目的。但是新的问题出现了，这种情况假如商户A模拟商户B的报文把商户B的钱转移走该怎么办？所以除了加密解密，还需要加签验签。
• 加签验签证明身份：加密已经完成，现在的问题只有怎么让银行区分这笔请求是商户A发的，还是商户B发的。想让银行区分出各个商户，拿出各个商户最独特的私钥加签即可，银行拿出对应的商户公钥验签即可。
• 到此，报文交互形成了一个稳定且安全的循环

带上代码设计一套加解密

结构

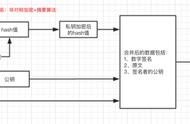
两对SHA1withRSA公私钥 DES会话密钥。结构如下：

加密加签步骤：

1. 使用KeyGenerator随机生成一个会话密钥desKey
2. 报文明文 会话密钥明文desKey对称加密得到加密后的密文message。
3. 银行的公钥 会话密钥desKey非对称加密得到加密后的会话密钥key。
4. 报文明文 商户的私钥非对称加密得到报文数字签名sign。
5. 将sign和key和message传递给银行。

解密验签步骤：

1. 加密后的会话密钥key 银行的私钥解密得到会话密钥明文desKey
2. 对称加密得到的密文message 会话密钥明文desKey解密得到报文明文
3. 得到的明文 商户的公钥验签，得到报文是否被中途篡改过

代码

1. 使用KeyGenerator随机生成一个会话密钥desKeyKeyGenerator keyGenerator = KeyGenerator.getInstance("DES"); SecretKey secretKey = keyGenerator.generateKey(); return secretKey.getEncoded();
2. 报文明文 会话密钥明文desKey对称加密得到加密后的密文message。public static String encryptContext(String context, byte[] desKey) throws Exception { byte[] encryptResult = des(context.getBytes("UTF-8"), desKey, 1); return Hex.encodeHexString(encryptResult); } private static byte[] des(byte[] inputBytes, byte[] keyBytes, int mode) throws Exception { DESKeySpec desKeySpec = new DESKeySpec(keyBytes); SecretKeyFactory keyFactory = SecretKeyFactory.getInstance("DES"); SecretKey secretKey = keyFactory.generateSecret(desKeySpec); IvParameterSpec iv = new IvParameterSpec(keyBytes); Cipher cipher = Cipher.getInstance("DES/CBC/PKCS5Padding"); cipher.init(mode, secretKey, iv); return cipher.doFinal(inputBytes); }
3. 银行的公钥 会话密钥desKey非对称加密得到加密后的会话密钥key/** * RAS加密 * * @return byte[]

*/

public byte[] encryptRSA(byte[] plainBytes, boolean useBase64Code, String charset)

throws Exception { String CIPHER_ALGORITHM = "RSA/ECB/PKCS1Padding"; // 加密block需要预留11字节 int KEYBIT = 2048; int RESERVEBYTES = 11; Cipher cipher = Cipher.getInstance(CIPHER_ALGORITHM); int decryptBlock = KEYBIT / 8; // 256 bytes int encryptBlock = decryptBlock - RESERVEBYTES; // 245 bytes // 计算分段加密的block数 (向上取整) int nBlock = (plainBytes.length / encryptBlock); if ((plainBytes.length % encryptBlock) != 0) { // 余数非0，block数再加1 nBlock = 1; } // 输出buffer, 大小为nBlock个decryptBlock ByteArrayOutputStream outbuf = new ByteArrayOutputStream(nBlock * decryptBlock); cipher.init(Cipher.ENCRYPT_MODE, peerPubKey); // 分段加密 for (int offset = 0; offset < plainBytes.length; offset = encryptBlock) { // block大小: encryptBlock 或 剩余字节数 int inputLen = (plainBytes.length - offset); if (inputLen > encryptBlock) { inputLen = encryptBlock; } // 得到分段加密结果 byte[] encryptedBlock = cipher.doFinal(plainBytes, offset, inputLen); // 追加结果到输出buffer中 outbuf.write(encryptedBlock); } // 如果是Base64编码，则返回Base64编码后的数组 if (useBase64Code) { return Base64.encodeBase64String(outbuf.toByteArray()).getBytes( charset); } else { return outbuf.toByteArray(); // ciphertext }

}

4. 报文明文 商户的私钥非对称加密得到报文数字签名sign。

/**

* RSA签名 * * @return byte[] * @throws Exception */

public byte[] signRSA(byte[] plainBytes, boolean useBase64Code, String charset) throws Exception {

Signature signature = Signature.getInstance("SHA1withRSA"); signature.initSign(localPrivKey); signature.update(plainBytes); // 如果是Base64编码的话，需要对签名后的数组以Base64编码 if (useBase64Code) { return Base64.encodeBase64String(signature.sign()).getBytes(charset); } else { return signature.sign(); }

}

5. 加密后的会话密钥key 银行的私钥解密得到会话密钥明文desKey；对称加密得到的密文message 会话密钥明文desKey解密得到报文明文

/**

* RSA解密 * * @param cryptedBytes * 待解密信息 * @return byte[] * @throws Exception */

public byte[] decryptRSA(byte[] cryptedBytes, boolean useBase64Code,

String charset) throws Exception { String CIPHER_ALGORITHM = "RSA/ECB/PKCS1Padding"; // 加密block需要预留11字节 byte[] data = null; // 如果是Base64编码的话，则要Base64解码 if (useBase64Code) { data = Base64.decodeBase64(new String(cryptedBytes, charset)); } else { data = cryptedBytes; } int KEYBIT = 2048; int RESERVEBYTES = 11; Cipher cipher = Cipher.getInstance(CIPHER_ALGORITHM); int decryptBlock = KEYBIT / 8; // 256 bytes int encryptBlock = decryptBlock - RESERVEBYTES; // 245 bytes // 计算分段解密的block数 (理论上应该能整除) int nBlock = (data.length / decryptBlock); // 输出buffer, , 大小为nBlock个encryptBlock ByteArrayOutputStream outbuf = new ByteArrayOutputStream(nBlock * encryptBlock); cipher.init(Cipher.DECRYPT_MODE, localPrivKey); // 分段解密 for (int offset = 0; offset < data.length; offset = decryptBlock) { // block大小: decryptBlock 或 剩余字节数 int inputLen = (data.length - offset); if (inputLen > decryptBlock) { inputLen = decryptBlock; } // 得到分段解密结果 byte[] decryptedBlock = cipher.doFinal(data, offset, inputLen); // 追加结果到输出buffer中 outbuf.write(decryptedBlock); } outbuf.flush(); outbuf.close(); return outbuf.toByteArray();

}

6. 得到的明文 商户的公钥验签，得到报文是否被中途篡改过

public boolean verifyRSA(byte[] plainBytes, byte[] signBytes,

boolean useBase64Code, String charset) throws Exception { Signature signature = Signature.getInstance("SHA1withRSA"); signature.initVerify(peerPubKey); signature.update(plainBytes); // 如果是Base64编码的话，需要对验签的数组以Base64解码 if (useBase64Code) { return signature.verify(Base64.decodeBase64(new String(signBytes, charset))); } else { return signature.verify(signBytes); }

}

代码只给出了一部分重要的加解密，加验签逻辑。还有一些逻辑都贴出来有点乱，就放在仓库里了，具体用法查看README即可，[更详细的参考放在demo里](https://gitee.com/metabolism/decry_eencrypt_mock) ### 思考：为什么RSA公钥加密的值一定只有私钥才能解开，不能暴力破解？？ 其实RSA的原理很简单，运用了数学的一个难题：两个大的质数相乘，难以在短时间内将其因式分解。原理很简单，但实际上操作真的很难。 ##### 时间复杂度--O 我们都知道计算机的计算速度非常快，计算几十位数的加减法都是秒出。 然而，虽然计算机很快，但再快也是有上限的。 比如我电脑的CPU主频是2.30GHz，也就是说我的电脑每秒可以进行2300000000次最基本的运行。  计算机的计算能力有限，就算是超级计算机“天河二号”，每秒也只能算3.39亿亿(这里多了个亿 ，给大佬跪了orz)次。 对应的，我们有一个参数来衡量一个程序的耗时，叫做时间复杂度： | 多项式量级 | 不严格的通俗例子(输入规模![[公式]](https://www.zhihu.com/equation?tex=n=10^9)) | | ------------------------------------------------------------ | ------------------------------------------------------------ | | 常量阶 ) | 只用1次运算,普通电脑 ![[公式]](https://www.zhihu.com/equation?tex=10^{-9}) 秒就能算完。 | | 对数阶 ) | 大约会用30次计算，普通电脑 ![[公式]](https://www.zhihu.com/equation?tex=10^{-8}) 秒算完 | | 线性阶 ) | ![[公式]](https://www.zhihu.com/equation?tex=10^9) 次计算，普通电脑需要一秒左右 | | 线性对数阶 ) | | | 平方阶 ),立方阶 ) | 大约是 ![[公式]](https://www.zhihu.com/equation?tex=10^{18}) 次计算，普通电脑大概要30年。 | | 非多项式量级 | 不严格的通俗例子(输入规模![[公式]](https://www.zhihu.com/equation?tex=n=10^9)) | | ------------------------------------------------------------ | ------------------------------------------------------------ | | 指数阶  | 大约2^1000000000次计算，心态崩了 | | 阶乘阶 n！ | 人类所有电脑加在一起，等太阳炸了都算不完 | 算法复杂度有各种各样的，有 ![[公式]](https://www.zhihu.com/equation?tex=O(1)) ， ![[公式]](https://www.zhihu.com/equation?tex=O(logn)), ![[公式]](https://www.zhihu.com/equation?tex=O(n)), ![[公式]](https://www.zhihu.com/equation?tex=O(n^2)), ![[公式]](https://www.zhihu.com/equation?tex=O(2^n))……上述几个复杂度的算法一个比一个慢。通俗的讲，大O后面括号里面**函数的增长速度越快，算法越耗时**。 总的来说，RSA之所以理论上非常安全，是因为破解RSA所要付出地计算成本远远高于使用RSA进行加密的计算成本。 * 使用RSA的私钥进行解密，耗用的时间复杂度是**多项式级**。 * 不使用RSA私钥，暴力破解，需要分解质因数，他的时间复杂度是**非多项式级**的**指数级**。 * 也就是有私钥解密只要一秒，暴力破解出结果时，人类可能已经毁灭了(不严格)。 ##### RSA生成公私钥数学计算流程： 1. 商户随机生成了一些非常非常大的整数，并用Miller-Rabin算法检测它们是不是质数，直到找到两个大质数——![[公式]](https://www.zhihu.com/equation?tex=p_1) 和 ![[公式]](https://www.zhihu.com/equation?tex=p_2) 。（随机数生成：多项式时间；Miller-Rabin: 多项式时间） 2. 商户计算两个质数的乘积 ![[公式]](https://www.zhihu.com/equation?tex=n=p_1p_2) （乘法: 多项式时间） 3. 商户计算 φ(n) = (p1 - 1)(p2 - 1) （乘法: 多项式时间），这一步难以被破解，因为n太大了，分解质因数需要指数级时间复杂度。人类毁灭前是根据n推算出φ(n)可能性极小。 * **欧拉函数：φ(n)表示：小于n的正整数中与n互质的数的数目。**（互质表示公因数为1） 比如想要知道φ(10)的话，我们就可以看[1, 10)中和10互质的整数，也就是1、3、7、9这四个数。（2、4、6、8和10有公因数2，而5和10有公因数10）。所以φ(10)=4。 比如想要知道φ(21)的话，我们就可以看[1, 21)中和21互质的整数，也就是1、2、4、5、8、10、11、13、16、17、19、20这12个数。（3、6、9、12、15、18和21有公因数3，而7、14和21有公因数7）。所以φ(21)=12。 4. 商户构造了一个比1大、比φ(n)小、不等于 ![[公式]](https://www.zhihu.com/equation?tex=p_1) 或 ![[公式]](https://www.zhihu.com/equation?tex=p_2) 的整数e。（随机数：多项式时间） 5. 商户求出了e对于φ(n)的乘法逆元d，也就是说**ed ≡ 1（mod φ(n)）**，也就是说ed=kφ(n) 1 (扩展欧几里得，多项式时间) 6. **请注意！现在神奇的事情发生了！对于一个与n互质的数a：** 因为 ![[公式]](https://www.zhihu.com/equation?tex=a^{φ(n)}≡1 ) (mod n) 所以 ![[公式]](https://www.zhihu.com/equation?tex=a^{kφ(n)}≡1) (mod n) 所以 ![[公式]](https://www.zhihu.com/equation?tex=a^{kφ(n)+1}≡a) (mod n) 所以 ![[公式]](https://www.zhihu.com/equation?tex=a^{ed}≡a) (mod n) 所以，若 ![[公式]](https://www.zhihu.com/equation?tex=c\equiv a^e) (mod n), 则![[公式]](https://www.zhihu.com/equation?tex=c^d\equiv a^{ed} \equiv a)（mod n） **到这里，两把钥匙构造完成！ㄟ(≧◇≦)ㄏ** **公钥：（n, e）** **密钥：（n, d）** ##### RSA公私钥加密解密 商户想要生成一对公私钥的时候： * 首先随意选择两个大的质数p和q，p不等于q，计算N=pq。 * 根据欧拉函数，求得r = (p-1)(q-1) * 选择一个小于 r 的整数 e，求得 e 关于模 r 的模反元素，命名为d。（模反元素存在，当且仅当e与r互质） * 将 p 和 q 的记录销毁。 * (N,e)是公钥，(N,d)是私钥。商户将她的公钥(N,e)传给银行，而将自己的私钥(N,d)藏起来。 商户进行加密的时候： * 假设商户想给银行送一个消息m，他知道银行的公钥，换句话说是银行公钥的N和e。他使用起先与银行约好的格式将m转换为一个小于N的整数n，比如他可以将每一个字转换为这个字的Unicode码，然后将这些数字连在一起组成一个数字。假如他的信息非常长的话，他可以将这个信息分为几段，然后将每一段转换为n。用下面这个公式他可以将n加密为c： ​ ne ≡ c (mod N) 计算c并不复杂。商户算出c后就可以将它传递给银行，也就是密文啦。 银行想要解密的时候： * 银行得到商户的密文消息c(商户使用银行公钥加密后的密文)后就可以利用他的私钥d来解码。他可以用以下这个公式来将c转换为n： cd ≡ n (mod N) 得到n后，他可以将原来的信息m重新复原。 ### 其他的概念 ##### 素数 素数又称质数，指在一个大于1的自然数中，除了1和此整数自身外，不能被其他自然数整除的数 ##### 互质数 互质，又称互素。若N个整数的最大公因子是1，则称这N个整数互质。 ##### 指数运算 指数运算又称乘方计算，计算结果称为幂。nm指将n自乘m次。把nm看作乘方的结果，叫做”n的m次幂”或”n的m次方”。其中，n称为“底数”，m称为“指数”。 ##### 模运算 模运算即求余运算。 ##### 同余 当两个整数除以同一个正整数，若得相同余数，则二整数同余。 ##### 会话密钥 前提：对称加密速度要比非对称加密快速。会话密钥是一个随机生成的对称式加密密钥，举个例子：A和B交互，A随机挑了一个字符串，用B的公钥加密发给了B，告诉B这个随机字符串就是他们之间用来交流的密钥了，之后A和B的报文就可以不用公私钥非对称加密，直接用这个密钥对称加密即可。对称式加密算法有很多：AES/DES等。SSH通信的数据就是用AES之类的对称式加密算法加密的。(在SSH协商密钥的过程中，还会使用专门的**密钥协商算法（Key Exchange Algorithm）**，确保窃听者无法偷听到密钥的内容) ##### 中间人攻击 即当商户发送公钥给银行的时候，黑客截取了商户的公钥，同时把自己公钥发给银行，这样一直在与银行通信的并不是商户。 ##### CA认证中心 专门提供网络身份认证服务的机构或团体 ### 总结 数学的魅力在于将这个世界变得井井有条，试想当计算机的运行速度越来越快，RSA会被破解吗？不见得，1999年N(两个大质数的乘积)位数是512，后面发展成了位数是1024和2048位，计算机速度变快之后，每台电脑能处理的位数也会越来越大，我相信我们会见到更长位数的N，十万，甚至百万.... 浩瀚世界，自己真渺小