说到加密,目前比较常见的有对称加密和非对称加密,那什么是对称加密和非对称加密呢,如图

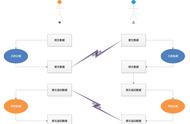
对称加密
假如 一个人A想把信息m发给B 他不能直接把m给B,不然会被窃听到,所以A经过一个算法,比如 e,得到C,
然后A把这个C发送给B,B收到C之后,通过 -e 的方式就得到了信息m
(例如: A想把数字 2 传给B, A通过 1的方式把 3 传给了B, B收到 3 之后,通过-1的方式就得到了 2 )

m 是明文,就是我们要传递的信息
e 是密钥,就是加密的算法,是需要保密的
C 是密文,就是加密之后的信息
这个C可以是公开的,但由于不知道你的密钥,所以就没有办法知道要传递的m
简单来说就是通过e加密,也通过e去解密
非对称加密
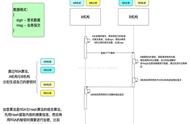
还是这个例子,一个人A想把信息m发给B,B生成了两个有关系的e 和 d ,e称为公钥,d称为私钥,B可以通过公开的方式把e发给A
A通过e里面的某一个算法 例如 e 对m进行加密得到C,A也可以通过公开的方式把C发送给B,不对称的就不对称到这,B收到之后通过不是通过-e的方式,而是-d的方式,得到了信息m
也就是说 通过e加密,然后用d去解密

RSA
其中一个最经典的非对称就是RSA加密算法,那这个RSA是基于什么原理,公钥e和私钥d有一个怎么样的关系呢
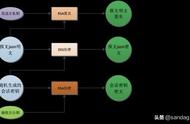
首先 B先找出两个质数 p和q
计算 n = p * q
φ(n) = (p-1) * (q-1) 这个函数又叫欧拉函数
公钥e 1 < e < φ(n) 在这个范围取出一个整数,并且 e 和 φ(n) 互质
私钥d (e * d ) / φ(n) = x ······ 1 (x是几无所谓,余数必须是1,比如 φ(n)是20 e是3 那么d就是7)
加密 m^e / n =x ······ c (这几个x都代表任意数的商,在这里面没有直接意义,可以忽略不看,这三个x也都不相等)
解密 c^d / n =x ······ m (可以从数学上证明,经过这一系列的计算,得到结果的余数一定是m)
安全性
首先我们先知道 A 和 B都知道哪些东西,B会把公钥e 和一个大数n 传给A,而B自己会留下一个私钥的d和一个相同的大数n,而A会把密文c传给B

由于n,e,c是知道的 是可以公开的,但是不知道私钥d,是很难破解出要传递的信息m的
那能不能通过公钥e去破解私钥d呢?
如果用e破解d,那么你首先知道φ(n)等于多少,想求出φ(n)的话,就必须知道 p 和 q
由n = p * q 我们也知道n,也知道p和q是质数,要求出p和q,这个过程是质因数分解
一个小数的质因数分解很简单(比如 21 = 3 * 7),但是一个大数的质因数分解却很难,更何况1024位的大数n呢(目前还没有人类能做出来)

由于这个原因,所以人们才认为RSA算法是比较保密的
那有没有什么方式可以快速的计算大数的质因数分解呢?
如果用我们普通的计算机去计算这个大数的质因数分解的话,大概需要10年的时间,才能算出来,当然如果用量子计算机的,可能一个星期就算出来了。
希望我的理解对您有所帮助!
,