作为金融时间序列的专题推文,【手把手教你】时间序列之日期处理主要介绍了使用Python处理时间序列的日期和统计分析;【Python量化基础】时间序列的自相关性与平稳性主要介绍了时间序列的一些基础概念,包括自相关性、偏自相关性、白噪声和平稳性;而【手把手教你】使用Python玩转金融时间序列模型主要介绍了AR、MA、ARMA和ARIMA模型的基本原理与Python的实现。从上一篇推文不难看出,使用ARMA等模型对股票收益率的时间序列建模效果不是很理想,主要在于忽略了时间序列的异方差和波动聚集特性。所谓波动性聚集,是指金融时间序列的波动具有大波动接着大波动,小波动接着小波动的特征,即波峰和波谷具有连续性。ARCH和GARCH模型正是基于条件异方差和波动聚集的特性建模的。本次推文着重介绍 ARCH和GARCH模型的基本原理及其Python实现。
02 股票收益率时间序列特点在介绍ARCH和GARCH模型之前,我们先来看看金融资产收益率的时间序列有哪些比较突出的特点。仍然以沪深300指数为例,考察其收益率时间的分布和统计特性。下面的Python代码与上一篇推文类似,包括导入需要用到的库、定义画图函数和使用tushare获取数据等。
import pandas as pd import numpy as np import statsmodels.tsa.api as smt #tsa为Time Series analysis缩写 import statsmodels.api as sm import scipy.stats as scs from arch import arch_model #画图 import matplotlib.pyplot as plt import matplotlib as mpl %matplotlib inline #正常显示画图时出现的中文和负号 from pylab import mpl mpl.rcParams['font.sans-serif']=['SimHei'] mpl.rcParams['axes.unicode_minus']=False def ts_plot(data, lags=None,title=''): if not isinstance(data, pd.Series): data = pd.Series(data) #matplotlib官方提供了五种不同的图形风格, #包括bmh、ggplot、dark_background、 #fivethirtyeight和grayscale with plt.style.context('ggplot'): fig = plt.figure(figsize=(10, 8)) layout = (3, 2) ts_ax = plt.subplot2grid(layout, (0, 0)) acf_ax = plt.subplot2grid(layout, (1, 0)) pacf_ax = plt.subplot2grid(layout, (1, 1)) qq_ax = plt.subplot2grid(layout, (2, 0)) pp_ax = plt.subplot2grid(layout, (2, 1)) data.plot(ax=ts_ax) ts_ax.set_title(title '时序图') smt.graphics.plot_acf(data, lags=lags, ax=acf_ax, alpha=0.5) acf_ax.set_title('自相关系数') smt.graphics.plot_pacf(data, lags=lags, ax=pacf_ax, alpha=0.5) pacf_ax.set_title('偏自相关系数') sm.qqplot(data, line='s', ax=qq_ax) qq_ax.set_title('QQ 图') scs.probplot(data, sparams=(data.mean(), data.std()), plot=pp_ax) pp_ax.set_title('PP 图') plt.tight_layout() return
使用tushare获取沪深300交易数据
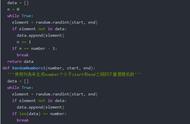
import tushare as ts token='输入你的token' pro=ts.pro_api(token) df=pro.index_daily(ts_code='000300.SH') df.index=pd.to_datetime(df.trade_date) del df.index.name df=df.sort_index() df['ret']=np.log(df.close/df.close.shift(1)) #df.head() ts_plot(df.ret.dropna(),lags=30,title='沪深300收益率')

从上图可以看出,沪深300指数收益率时间序列呈现出以下几个现象,具有一定的普遍性。
- 自相关性比较弱,但对其进行变换后,如取平方、绝对值等,则表现出很强的自相关性(见后文);
- 收益率的条件方差(Conditional Variance)随着时间而变化,即存在条件异方差的特征。
- 收益率序列的波动具有持续性,即存在波动集聚(Volatility Clustering)的现象。比如2007-2008、2015-2016、2019具有较大的波动性。
- QQ图显示,收益率并不服从正态分布,极端值较多,具有厚尾的现象。
ARCH模型全称是自回归条件异方差模型,Autoregressive Conditionally Heteroskedastic Models - ARCH(p),是Engle在1982年分析英国通货膨胀率时提出的模型,主要用于刻画波动率的统计特征。
一般先假设收益率序列满足某个经典时间序列模型(MA、AR或ARMA),以AR(1)模型为例:

收益率yt的波动率(条件方差)可以使用残差项的波动率进行刻画:
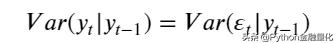
为了刻画资产收益率的这种波动特性,可以令残差项的条件方差与过去残差项的平方相关。因此,ARCH(p)模型可以表示为: