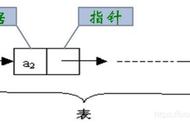
如图所示为线性表(a, b, c, d, e) 后插法的创建过程,读入数据的顺序和线性表中的逻辑顺序是相同的。

【算法代码】
LinkedList LinkedListCreateByTail(LinkedList slist, ElemType elem)
{
if (nullptr == slist)
{
cout << "链表未初始化" << endl;
return nullptr;
}
else
{
LinkedListNode* header = slist;
LinkedListNode* clist = slist;
while (nullptr != clist->next)
{
clist = clist->next;
}
LinkedListNode* node = (LinkedListNode*)malloc(sizeof(LinkedListNode));
if (nullptr == node)
{
cout << "创建结点失败" << endl;
return nullptr;
}
else
{
node->data = elem;
node->next = nullptr;
clist->next = node;
return header;
}
}
}单链表的取值
单链表与顺序表不同,其逻辑相邻的结点并没有存储在物理相邻的单元中。根据给定的结点位置序号i访问该结点的值是行不通的,只能从链表的首元结点出发,顺着链域next逐个结点向下访问。
【算法代码】
LinkedListNode* GetLinkedListNode(LinkedList slist, int pos)
{
if (nullptr == slist)
{
cout << "空链表" << endl;
return nullptr;
}
else if (pos <= 0)
{
cout << "输入位置错误" << endl;
return nullptr;
}
else
{
LinkedListNode* clist = slist;//当前结点
for (int i = 0; i < pos && clist->next != nullptr; i)
{
clist = clist->next;
}
return clist;
}
}单链表的查找
链表中按值查找的过程和顺序表类似,从链表的首元结点出发,依次将结点值和给定值elem进行比较,返回查找结果。
【算法代码】LinkedListNode* LocateLinkedListNode(LinkedList slist, ElemType elem)
{
if (nullptr == slist)
{
cout << "空链表" << endl;
return nullptr;
}
else
{
LinkedListNode* clist = slist->next;//当前结点
while (clist && elem != clist->data)
{
clist = clist->next;
}
return clist; //查找成功返回值为elem的结点地址, 查找失败p为NULL
}
}单链表的插入
单链表插入新结点时,根据插入的位置不同,分为以下3种情况:
- 插入到链表的头部(头节点之后),作为首元节点。
- 插入到链表中间的某个位置。
- 插入到链表的尾部,作为链表中最后一个数据元素。
虽然新元素的插入位置不固定,但是链表插入元素的思想是固定的,只需做以下两步操作,即可将新元素插入到指定的位置:
- 将新结点的 next 指针指向插入位置后的结点;
- 将插入位置前结点的 next 指针指向插入结点;
例如,在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5,其实现过程如图所示:

注意:链表插入元素的操作必须是先步骤 1,再步骤 2;反之,若先执行步骤 2,除非再添加一个指针,作为插入位置后续链表的头指针,否则会导致插入位置后的这部分链表丢失,无法再实现步骤 1。
【算法代码】
LinkedList LinkedListInsert(LinkedList slist, ElemType elem, int pos)
{
if (nullptr == slist)
{
cout << "空链表" << endl;
return nullptr;
}
else
{
LinkedListNode* header = slist;//头结点
LinkedListNode* clist = slist;//当前结点
for (int i = 1; i < pos && nullptr != clist->next; i)
{
clist = clist->next;
}
LinkedListNode* node = (LinkedListNode*)malloc(sizeof(LinkedListNode));
if (nullptr == node)
{
cout << "创建结点失败" << endl;
return nullptr;
}
else
{
node->data = elem;
node->next = clist->next;
clist->next = node;
return header;
}
}
}
单链表的插入操作虽然不需要像顺序表的插入操作那样需要移动元素,但平均时间复杂度仍
为。
单链表的删除从链表中删除指定数据元素时,实则就是将存有该数据元素的节点从链表中摘除,同插入元素一样,首先应该找到该位置的前驱结点。
例如,从存有{1, 2, 3, 4}的链表中删除元素3,则此代码的执行效果如图所示:

其中,从链表上摘除某节点的实现非常简单,只需找到该节点的直接前驱节点 temp,执行一行程序:
clist->next= clist->next->next;
但在删除数据元素3结点时,除了修改数据元素2结点的指针域外,还要释放数据元素3的结点所占的空间,所以在修改指针前,应该引入另一指针tlist, 临时保存数据元素3结点的地址以备释放。
【算法代码】
LinkedList LinkedListDelete(LinkedList slist, ElemType elem)
{
if (nullptr == slist)
{
cout << "空链表" << endl;
return nullptr;
}
else
{
bool FindFlag = false;
LinkedListNode* header = slist;//头结点
LinkedListNode* clist = slist;//当前结点
LinkedListNode* tlist = nullptr;
while (nullptr != clist->next)
{
if (elem == clist->next->data)
{
tlist = clist->next;
clist->next = clist->next->next;
free(tlist);
tlist = nullptr;
FindFlag = true;
break;
}
else
{
clist = clist->next;
}
}
if (!FindFlag)
{
cout << "未找到该元素: " << elem << endl;
}
return header;
}
}
类似于插入算法,删除算法时间复杂度亦为。
获取链表长度遍历链表中每一个结点,直到指针域next为空结束,则遍历的次数就是链表的长度。
【算法代码】
int GetLinkedListLength(LinkedList slist)
{
LinkedListNode* p = slist->next;
int length = 0;
while (p)
{
length;
p = p->next;
}
return length;
}完整代码
Github:https://github.com/MrYuxiangZhu/DataStructure/tree/master/01. LinkedList
,