二叉搜索树的局限性
上一节较为详细的介绍了C语言中的二叉搜索树,提到数据采取二叉搜索树的结构存储,可以获得不错的搜索性能。

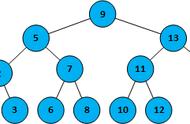
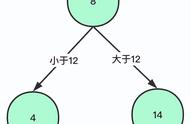
二叉搜索树之所以有不错的搜索效率,是因为在往树中插入数值时,始终严格的遵守左子节点值比父节点值小,右子节点值比父节点大的准则。以搜索 12 为例:
从根节点开始, 12 比 9 大,所以转向右节点; 12 比 29 小,所以转向左节点; 查找完毕。
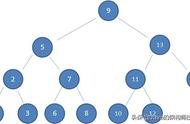
这样就避免了遍历所有数值。稍微思考一下应该能发现,当二叉搜索树的每个节点都有两个子节点时,树才是最优的,这时二叉搜索树才能在存储尽可能多数值的同时,保留优秀的搜索性能。为什么呢?我们考虑一下极端情况,假设所有节点(除了最后一个节点)都只有一个子节点,如下图:

这种情况的二叉树就是一个链表了,搜索时只能像链表一样线性遍历,丢失了二叉树应有的搜索性能。
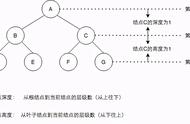
自平衡二叉搜索树为了解决二叉搜索树的这种缺陷,自平衡二叉搜索树就被提出了。平衡二叉搜索树本质上也是一个二叉搜索树,只不过它的所有叶子节点深度差不超过 1。

节点的深度是指从根节点起,达到它一共需要经过的父节点数目。处于树最末端的节点称为叶子节点。
按照之前的分析,上图右图显然比上图作图具备更优异的性能。
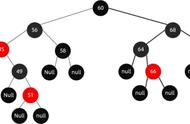
红黑树虽然自平衡二叉树更能发挥二叉搜索树的优异搜索特性,但是维护起来却非常的麻烦,很难保证插入新数据的时候也具备不错的效率,所以红黑树就被提出了。一个典型的红黑树结构如下图: