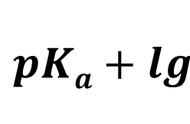太阳的视星等被定义为-26.74,我想知道计算这个的准则是什么,-26.74是如何被测算出来的?这个方法可以用来测量其他光谱类型的星体的视星等吗?

“视星等”的说法可以追溯到希腊的天文学家希帕克斯。他望着天上的星星,按照亮度来把它们分类。看起来最亮的星为一级,二级比一级暗一点,六级则是我们看见的光最为微弱的星星,这是我们沿用至今已有两千余年的分类准则。
这个方法看起来很好很简单,但是它的结果不能很好的与星体实际亮度相对应。因为人类的眼睛观察的亮度会产生很大的差异,并且让这些差异变得更小。

因此,你可能会认为视星等分级设置是“正确”的,一级星和二级星所产生的光线之间的区别会与二级星和三级星所产生的光线之间的区别一样——这就是所谓的线性亮度比。然而,当我们测量所接收到的星星产生的光有多亮时,(使用精密仪器,如数码相机或耦合器)我们会发现不同的视星等之间的亮度比率是常数。

这就是说,二级视星等大约比一级暗2.5倍,并且三级视星等比二级暗2.5倍因此是比一级暗2.5*2.5≈6.5倍,一直到六级视星等(希帕克斯所看到的最暗的星星)我们发现六级视星等比一级大概暗100倍。这种类型的现象特征就是所谓的亮度对数。

到现代,我们对希帕克斯的定义进行调整,使其更精确更方便。因此,我们现在定义五个“量级”的差异正好是100的亮度比。此外,我们把整个规模与被定义为0级视星等(或者说非常接近0,不管怎么说,现代的精确地测量把织女星的视星等定义为0.03级,但是这是一个技术点)的织女星联系起来。最后,尽管希帕克斯的方法只能定义一到六级视星等,我们不对其进行任何限制——可以出现比织女星更亮的甚至为负数的视星等。(我大学时的一位天文教授曾推测,也许希帕克斯在观察天上的星星时,只看了一方的天空,当他转身看见一颗更亮的像是织女星的星星时,于是他说:“哎呀,我想我们得把他的视星等设置为0”)
以上混乱讨论的结果是,我们得到了任意两个星星的亮度和大小的公式
F2 / F1 = 100(m1 - m2) / 5
或者
m1 - m2 = -2.5 log10 ( F1 / F2)
在上述式中,F1和F2是我们用耦合器所测量的到的两个星星的亮度或流量,同时m1和m2是两颗星的视星等。所以我们发现太阳的视星等是-26.74的方法是测量在地球上看它有多亮,然后观察到我们从太阳接收到的光是织女星的510倍,在上面的公式中带入F1/F2的比值我们得到太阳的视星等是-26.74。

需要指出的是,视星等并不能用来测量它的实际亮度,而是我们能看到的亮度,也取决于这些星星离我们的距离有多远。(这就是为什么尽管太阳只是一个普通的星星而它的视星等却是这么极端特别。)我们也可以定义所谓的绝对视星等,即测量物体的实际亮度。它被定义为一个物体距离我们10秒差距,太阳的绝对视星等是4.83。

解答你最后的问题,上述公式可以用于任何恒星,不管它们的光谱类型和颜色是何种。然而,恒星有不同颜色的事实意味着,给定的两个星星之间的亮度比率可能会随着你所观察的颜色而改变。因此,每个星星的视星等也取决于它们的光的颜色。所以,当我们引用一颗恒星的视星等时,我们必须准确的定义我们所看到的光类型。在上面的文章中,我们讨论了“视觉”或“V波段”的视星等,它对应于与眼睛最敏感的光(黄绿色)相似的光来测量的视星等。要了解一些关于表观视星等系统利弊的观点(尽管它很复杂,但优点比你想象的要多),请看这篇来自基特峰国家天文台的史蒂夫·怀特的文章。
参考资料
1.Wikipedia百科全书
2.天文学名词
3. Dave Rothstein- astro- dulzura
如有相关内容侵权,请于三十日以内联系作者删除
转载还请取得授权,并注意保持完整性和注明出处