小数乘法
1、小数乘整数
意义:求几个相同加数的和的简便运算。如,1.5×3表示1.5的3倍是多少或3个1.5是多少。
计算方法:先把小数扩大成整数,按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
2、小数乘小数
意义:求这个数的几分之几是多少。如,1.5×0.8(整数部分是0)就是求1.5的十分之八是多少。1.5×1.8(整数部分不是0)就是求1.5的1.8倍是多少。
计算方法:先把小数扩大成整数,按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位。
3、规律:一个数(0除外)乘大于1的数,积比原来的数大; 一个数(0除外)乘小于1的数,积比原来的数小。
4、求近似数的方法一般有三种:四舍五入法;进一法;去尾法。
5、计算钱数时保留两位小数,表示计算到分。保留一位小数,表示计算到角。
6、小数四则运算顺序跟整数是一样的。
7、运算定律和性质:
加法交换律:a b=b a
加法结合律:(a b) c=a (b c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a b)×c=a×c b×c或a×c b×c=(a b)×c(b=1时,省略b)
变式: (a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c
减法性质:a-b-c=a-(b c)
除法性质:a÷b÷c=a÷(b×c)
位置
确定物体的位置,要用到数对。用数对能解决两个问题:一是给出一对数对,能在坐标中标出物体所在位置的点。二是给出坐标中的一个点,能用数对表示。
小数除法
1、小数除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算。如,0.6÷0.3表示已知两个因数的积是0.6,一个因数是0.3,求另一个因数是多少。
2、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点应和被除数的小数点对齐。整数部分不够除,商0,点上小数点。如果有余数,要添0再除。
3、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
4、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
5、除法的变化规律:
(1)商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。
(2)除数不变,被除数扩大(缩小),商随着扩大(缩小)。
(3)被除数不变,除数缩小,商反而扩大;被除数不变,除数扩大,商反而缩小。
6、循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。
循环节:一个循环小数的小数部分,依次不断重复出现的数字。如,6.3232……的循环节是32。
7、小数部分的位数是有限的小数,叫做有限小数。小数部分的位数是无限的小数,叫做无限小数。小数分为有限小数和无限小数。
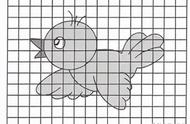
可能性
1、事件发生有三种情况:可能发生、不可能发生、一定发生。
2、把几种可能的情况的份数相加做分母,单一的这种可能性做分子,就可求出相应事件发生的可能性大小。
简易方程
1、在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。加号、减号、除号以及数与数之间的乘号不能省略。
2、a×a可以写作a·a或a^2,读作a的平方;2a表示a a。
3、方程:含有未知数的等式称为方程(方程必须满足两个条件,一是等式,二是有未知数)。使方程左右两边相等的未知数的值,叫做方程的解。求方程的解的过程叫做解方程。
4、解方程原理:天平平衡。 等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
5、数量关系式:
和=加数 加数
一个加数=和-另一个加数
差=被减数-减数
被减数=差 减数
减数=被减数-差
积=因数×因数
一个因数=积÷另一个因数
商=被除数÷除数
被除数=商×除数
除数=被除数÷商
多边形的面积
1、公式:
多边形
面积公式
面积公式的变式
正方形
正方形的面积=边长X边长
已知正方形的面积,求边长
长方形
长方形的面积=长X宽
已知长方形的面积和长,求宽
平行四边形
平行四边形的面积=底X高
已知平行四边形的面积和底,求高
三角形
三角形的面积=底X高÷2
已知三角形的面积和底,求高
梯形
梯形的面积=(上底 下底)X高÷2
已知梯形的面积与上下底之和,求高
高=面积×2÷(上底 下底)
上底=面积×2÷高-下底
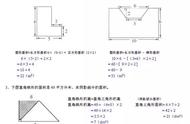
组合图形
当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。
当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
2、平行四边形面积公式推导:剪拼、平移
平行四边形可以转化成一个长方形,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高, 长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
3、三角形面积公式推导:旋转
两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底,平行四边形的高相当于三角形的高。
平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2。
4、梯形面积公式推导:旋转
两个完全一样的梯形可以拼成一个平行四边形,平行四边形的底相当于梯形的上下底之和,平行四边形的高相当于梯形的高,平行四边形的面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底 下底)×高÷2
5、等底等高的平行四边形面积相等,等底等高的三角形面积相等,等底等高的平行四边形面积是三角形面积的2倍。
6、长方形框架拉成平行四边形,周长不变,面积变小。
7、组合图形面积计算可以转化成已学的简单图形。
当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算;
当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算。
植树问题
1、不封闭栽树问题:
(1)一条路的一边两端都栽树:路长÷间隔 1;已知间隔数,树的棵树,求路长。路长=间隔数×(树的棵树-1)
(2)一条路的两边两端都栽树:(路长÷间隔 1)×2
(3)一条路的一边两端不栽树:路长÷间隔-1
(4)一条路的两边两端不栽树:(路长÷间隔-1)×2
(5)锯木头时间问题:锯一段木头时间=总时间÷(段数-1)
2、封闭图形四周栽树问题:栽树棵树=周长÷间隔
3、鸡兔同笼问题(龟鹤问题、大船小船问题):
(1)算术假设法1:假设都是兔子,先求鸡的只数
鸡的只数:(总头数×4-总脚数)÷(4-2)
兔的只数:总头数-鸡的只数
算术假设法2:假设几只都是鸡,先求兔子的只数
兔子的只数:(总脚数-总头数×2)÷(4-2)
鸡的只数:总头数-兔子的只数
(2)方程法:设兔子有x只,则兔子脚有2x只。那么鸡有(总头数-x)只,根据“兔子脚 鸡脚=总脚数”列方程解答。
即:4x 2×(总头数-x)=总脚数
,