三角形问题是初中数学中非常重要的部分,题型变化多样。我们在前面的文章中介绍了三角形的高线求角度问题,那么关于三角形的高线除了求角度问题以外,还有哪些作用需要我们掌握呢?等面积法常用来求线段之间的数量关系,比如最常见的数量之间的和差关系。考试中遇到的大部分题目源于教材又高于教材,往往需要我们先吃透教材,并且善于反思、思考,总结解题方法,从而能够做到举一反三。

例题1:已知直角三角形的三边长分别为3、4、5,求斜边上的高
分析:已知直角三角形的三边长,由于直角三角形中斜边最长,可以判定3、4为直角边,5为斜边,由此根据三角形的面积公式可求出面积。除了将两直角边看作底和高,也可以将斜边看作底,利用面积相等,即可求出斜边上的高。

这是等面积法最直接的使用,即求直角三角形斜边上的高,到初二会与勾股定理、特殊四边形等知识点相结合,因此首先要熟悉基础知识点的推导过程,再灵活运用。
类型二:求线段的比值例题2:在△ABC中,AB=7,AC=5,BC=9,BE⊥AC,AD⊥BC,求AD与BE之间存在着怎样的数量关系?
分析:求AD与BE的数量关系,可以利用面积相等,由BE⊥AC、AD⊥BC可得到两种关于三角形面积的表达方式,然后代入数据即可得到AD与BE之间的数量关系。

有垂直想高线,利用面积相等建立等式,代入已知条件求出不同高之间的关系。

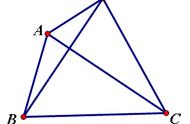
例题3:如图,在等腰三角形ABC中,点P为底边AB上任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D,求证:PE PF=AD。
分析:根据等腰三角形的性质及三角形的面积公式就可以求出等腰三角形的腰上的高与底边上的点到两腰的距离之和的关系,由此可以得到结论:等腰三角形腰上的高等于底边上的点到两腰的距离之和。

那么,当点P在三角形ABC内部时,又有什么结论呢?即点P在等边三角形ABC内,PE⊥AB,PF⊥AC,PG⊥BC,PE、PF、PG、BD之间的数量关系为:BD=PE PG PH。

利用等面积法可以求解这三类问题:(1)借助面积求线段的长度;(2)借助面积求线段的比值;(3)借助面积求线段的和差关系。
,