零是有理数还是无理数,什么叫有理数和无理数

然而，这个传说未必可信，毕达哥拉斯学派有许多严格且奇怪的规矩，比如“禁食豆子”，“东西落下了，不要用手拣起来”等等，最重要的是，在毕达哥拉斯建立的团体中，财产是公有的，而且学派的成员们有一种共同的生活方式，甚至于科学和数学的发现也被认为是集体的，所以更可能的情形是——希帕索斯因违反了毕达哥拉斯学派的规矩而被驱逐出学派。

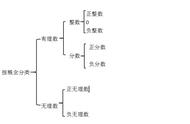
因此认为无理数是“没有道理的数”实际上是对其的误解。同有理数一样，无理数的命名也是源于翻译问题。实际上，无理数的英文为irrational number，irrational的原意是“不可比的”或“不能表达成比率的”。所谓的“无理数”，不过是“无比数”的误译而已。

无理数无法写成两个整数之比，最著名的例子莫过于对是无理数的证明，其方法是反证法，我们可以假设是一个有理数，即它可以写成两个互素的整数之比

则

则必为一偶数，因此必为一偶数，令

则

则必为一偶数，必为一偶数，则都为偶数，这一结论是荒谬的，因为我们已经假设了是互素的，而两个偶数不可能互素，它们至少还有公因数2，因此假设不成立，是无理数得证。

其中在生活中，我们也离不开无理数。比如你拿一张日常生活中随处可见的A4纸，其长宽之比即约为

而将其对折后，长宽之比仍然为

继续折，无论你折多少次，你得到的永远是“型纸”！这个数，永远都“折”不掉！因为只有这个数才具备这个神奇的性质。

还有著名的黄金分割比

也是一个无理数，其大量存在于绘画、建筑、艺术作品中。