这一阵各大新闻媒体谈到新型肺炎疫情时都会频繁使用一个词“拐点”。全国上下都在期盼疫情的拐点快快到来。到底什么是疫情的拐点?怎样从走势图上看出拐点?许多朋友一脸懵逼。我作为海归美国物理学博士,希望尽自己微薄之力,为广大网友做一个尽可能浅显易懂的解释。具备高中数学知识应该都能理解。

源于网易
首先“疫情的拐点”这个概念非常模糊。国家发布的统计数据有确诊、疑似、死亡、治愈病例等不同类别。是用某一条曲线代表疫情的发展,还是综合起来分析?大家可以保留各自的观点。我这里选择以确诊病人统计为准。因为我觉得它最具代表性:“确诊”相对“疑似”更为确定,相对“死亡”和“治愈”更为及时。同时仅看“确诊”一条曲线也简化了问题,便于理解。

大学数学 南京大学出版社陈仲

拐点定义 大学数学 陈仲

函数凸性与拐点 大学数学 陈仲
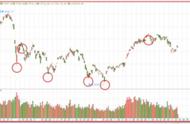
下面的图1是根据国家统计截止2月6日绘制的确诊人数函数。今日头条app的“抗击肺炎”频道也有类似统计图。我们可以看出确诊人数一直在增长。现阶段专家们并不奢求增长会停止,而是希望出现一个拐点。直观的讲,拐点意味着从某一天开始确诊人数增长趋势在减缓,疫情得到了有效控制。怎样从图中找出拐点来呢?一切要从最基本的数学定义出发。目前网络如此发达,拐点的定义随便一搜便有。但为了严谨,我翻箱倒柜找出了自己十几年前在南京大学读本科时陈仲教授讲课用的大学数学教材。参考上面的课本截图,简单的说拐点满足的条件是:二阶导数在拐点处异号(由正变负或由负变正)。不要被高等数学复杂的定义吓倒,我接下来的解释非常通俗易懂。

图1 累计确诊人数函数 源于网易

图2 新增确诊人数函数 源于网易
下面我向大家介绍一种仅凭目测就能找出拐点的方法。图2是新增确诊人数的函数,可以近似看做是图1累计函数的一阶导数。利用它即可看出拐点,并不需要画出二阶导数图。我们只需要找到新增确诊人数走势的转折点——即从上坡( 号)变为下坡(-号)的地方。从图2可以看出A点1月27日的左侧是上坡,右侧是下坡。即对应于图1的A点左侧二阶导数为正,右侧为负。按上述定义可以得A为拐点。再看看图1,仔细观察你会发现坡度在A点变缓了。若想深入了解,函数在A点的形态对应于前面教材截图里函数凸性的上升、上凸(红色方框中),表示增长逐渐变缓。同理按上述方法我们可以找出A,B,C三个拐点。什么?你告诉我目前疫情已经出现了三个拐点?瞎扯,新闻为啥没报?别急,这只是根据数学定义得出的结论。实际上虽然1月27日出现了拐点,但是又让1月28日那个由负到正的“反向”拐点B点拐回去了……感觉遇到了一个假拐点,没有实际的意义。可喜的是根据2月7日最新数据可以判断2月4日又出现了新的拐点C。但这也许是暂时的,有可能会像1月28日那样拐回去。所以现在说2月4日是整个疫情的拐点为时尚早。如果接下来新增确诊人数持续走下坡路,我们就可以确定拐点出现了,因为确诊人数增长趋势变慢了。有兴趣的读者可以用我讲的方法试试疑似、死亡和治愈人数的曲线,看能否找到各自的拐点?拐点的出现仅仅是曙光。最终我们希望图2的曲线能一直走下坡路,降到0。届时图1累计确诊曲线将成为一条水平线,意味着确诊人数不再增加。那才是全国人民的最后胜利!
作者特此声明:本文并不是发布拐点、预测拐点,而仅仅从数学对拐点的定义去解释、探讨拐点。全文仅代表我个人的观点。至于什么时候出现疫情拐点一定要以国家权威机构的消息发布为准。
,