他的证明属于公元前 350 年左右的古希腊数学家 欧几里德。我们将证明,如果我们列出素数 p1、p2、p3 等,这个列表会一直持续下去吗?
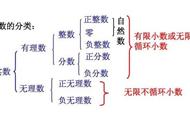
但首先我们需要熟悉数字的术语……例如什么是整数?
我们在整个学校生活中熟悉的数字和整数有什么区别?
数字是用于计数、测量和标记的数学对象。原始示例是自然数1、2、3、4 等。
数字 ....,-3,-2,-1,0,1,2,... 称为有理整数或简称为“整数”。
数字 0,1,2,... 是非负整数,数字 1,2,3 是正整数。正整数通常是必不可少的,可以将它们视为整数的子类或更大的数字类。
什么是数的整除率?一个整数 a 被另一个整数 b 整除,而不是 0,如果存在第三个整数 c 使得 a=bc。我们表示 a 可以被 b 整除,或者 b 是 a 的约数,表示为b|a 因此 1|a ; a|a 和 b|0 对于除 0 之外的每个 b。
当我们表示 b ∤ a 时,它意味着 b|a 相反。
很明显 b | a 和 c | b ➡️ 这意味着 c | A。(来自过渡属性)
如果 c | b 和 c | a 这意味着 c 也是 b 和 a 的线性组合的除数,所以从代数性质 c | ma nb 如果 c 不等于 0 并且对于所有整数 m 和 n。
素数的奥秘是什么?
素数对我来说总是很神秘♀️。
当我拿着数字时,我保留了素数,因为它们很神秘,而且奇怪地让我感觉更好。
素数是一个特别重要的子类,素数类。
如果 p 满足(i)和(ii) ,则素数满足如果数字 p 是素数
(i) p>1
(ii)除了 1 和 p 之外,p 没有正因子。
大于 1 且不是素数的数称为合数。
为什么数字 1 不是质数?我找到了一个令人信服的答案,回答了我在高中时问过老师的一个问题。为什么 1 不是质数?
(i) 如果把它看作一个素数,那么,其他所有自然数都是它的倍数。
我们称 (ii) 作为算术基本定理指出每个大于 1 的整数都可以唯一地表示为素数的乘积,直到因子的顺序,而不是 6=2x3 是复合的唯一因式分解数字 6,另一种选择是 6=1x2x3 或 6=1x1x2x3。所以如果 1 是质数,因式分解将不再是唯一的。
(iii)定义什么是质数会变得相当困难。毕竟 2=1x2 会表明 2 除了自身之外还有一个质因数,即 1。但是我们仍然希望 2 被视为质数,因此我们必须将“自身”排除在外。而且 1 仍然只会将“自身”作为一个因素。
为什么有无穷多个素数?我们从所有素数的列表开始,假设我们已经到达某个阶段 n,n 可以是十、一百万、十亿、一万亿,等等。
我们达到了某个阶段,我们证明我们总能找到另一个比上一个更大的素数。对于任何有限集 n= (p1 x p2 x p3 一直到 pr) 我们考虑数 n=p1 x p2 x p3 x..x pr 1 肯定比该序列中的最后一个大。
所以如果 n 是质数,那么它是比 pr 大的质数。我们并不是说 n 会是 pr 之后的下一个素数,事实上它几乎肯定不会是因为 n 比这些数字大得多。
所以 n 有一个素数除数 p,但 p 不是 pi 之一,否则 p 将是 n 和乘积 p1x p2 x p3 x..x pr 的除数,因此也是差值 n- p1 x p2 x p3 的除数x..x pr = 1 这是不可能的。如果它与一个不同,则它大于 pr 。
我们找到了一个比 pr 大的素数。这个素数 p 是 pr 之后的下一个素数吗?..是的.
所以有限集{p1,p2,….,pr}不可能是所有素数的集合。
关键是我们找到了一个比 n 大的素数,所以再一次,列表可以继续。以这种方式定义 n 以确保如果存在除 n 的质数,它不会等于其中任何一个。
,