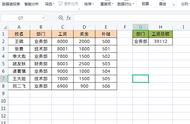
模块一:勾股定理
1.定义:在平面上的一个直角三角形中,两个直角边边长的平方加起来等于斜边长的平方。如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:


几何图如图所示
也称商高定理(西周),赵爽弦图(三国),勾股圆方图(九章算术),百牛定理(古希腊),毕达哥拉斯定理(古希腊)
eg:
以上图的直角三角形为例,a的边长为3,b的边长为4,则我们可以利用勾股定理计算出c的边长。
由勾股定理得,a b = c → =
即,9 16 = 25 = c²
c = 5
所以我们可以利用勾股定理计算出c的边长为5。
2.证明
邹元治证法:

赵爽弦图: