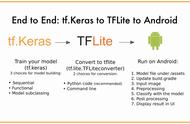
风控业务背景
在风控中,稳定性压倒一切。原因在于,一套风控模型正式上线运行后往往需要很久(通常一年以上)才会被替换下线。如果模型不稳定,意味着模型不可控,对于业务本身而言就是一种不确定性风险,直接影响决策的合理性。这是不可接受的。
本文将从稳定性的直观理解、群体稳定性指标(Population Stability Index,PSI)的计算逻辑、PSI背后的含义等多维度展开分析。
目录
Part 1. 稳定性的直观理解
Part 2. 群体稳定性指标(Population Stability Index,PSI)的理解
Part 3. 相对熵(KL散度)的理解
Part 4. 相对熵与PSI之间的关系
Part 5. PSI指标的业务应用
Part 6. PSI的计算代码(Python)
Part 1. 稳定性的直观理解
在日常生活中,我们可能会看到每月电表、水表数值的变化。直观理解上的系统稳定,通常是指某项指标波动小(低方差),指标曲线几乎是一条水平的直线。此时,我们就会觉得系统运行正常稳定,很有安全感。
在数学上,我们通常可以用变异系数(Coefficient of Variation,CV)来衡量这种数据波动水平。变异系数越小,代表波动越小,稳定性越好。
变异系数的计算公式为:变异系数 C·V =( 标准偏差 SD / 平均值Mean )× 100%
那么,是不是只用用变异系数就可以了呢?方便、直观。——答案是否定的。在机器学习建模时,我们基于假设“历史样本分布等于未来样本分布”。因此,我们通常认为:
模型或变量稳定 <=> 未来样本分布与历史样本分布之间的偏差小。
然而,实际中由于受到客群变化(互金市场用户群体变化快)、数据源采集变化(比如爬虫接口被风控了)等等因素影响,实际样本分布将会发生偏移,就会导致模型不稳定。
Part 2. 群体稳定性指标(Population Stability Index,PSI)的理解
如果你有基础的风控建模经验,想必会很熟悉PSI(Population Stability Index)指标。psi反映了验证样本在各分数段的分布与建模样本分布的稳定性。在建模中,我们常用来筛选特征变量、评估模型稳定性。
那么,PSI的计算逻辑是怎样的呢?很多博客文章都会直接告诉我们,稳定性是有参照的,因此需要有两个分布——实际分布(actual)和预期分布(expected)。其中,在建模时通常以训练样本(In the Sample, INS)作为预期分布,而验证样本通常作为实际分布。验证样本一般包括样本外(Out of Sample,OOS)和跨时间样本(Out of Time,OOT)。
我们从直觉上理解,是不是可以把两个分布重叠放在一起,比较下两个分布的差异有多大?

图 1 - 分数分布差异对比
PSI的计算公式也告诉我们,的确是这样的:
(1)psi=∑i=1n(Ai−Ei)∗ln(Ai/Ei)
PSI = SUM( (实际占比 - 预期占比)* ln(实际占比 / 预期占比) )
大多数同学到了这里,遵循拿来主义,直接应用。但是,大家有没有思考过以下几个问题:
Q1: 为什么要在计算公式中引入对数—— ln(实际占比 / 预期占比)?
Q2: 为什么log的底数是自然常数e,而不是其他常数(比如2)?(信息论中基常常选择为2,因此信息的单位为比特bits;而机器学习中基常选择为自然常数,因此单位常被称为奈特nats)
Q3: 如果只是衡量两个分布的差异,为什么不直接定义成以下公式呢?这个公式含义是把各个分数段里的人群占比差异进行累加放大。
自定义的稳定性指标 = SUM(实际占比 - 预期占比)
让我们先保留这些疑问,回到PSI的计算公式,以图2表格数据为例介绍下计算步骤。
- step1:将变量预期分布(excepted)进行分箱(binning)离散化,统计各个分箱里的样本占比。
注意:
a) 分箱可以是等频、等距或其他方式,分箱方式不同,将导致计算结果略微有差异;
b) 对于连续型变量(特征变量、模型分数等),分箱数需要设置合理,一般设为10或20;对于离散型变量,如果分箱太多可以提前考虑合并小分箱;分箱数太多,可能会导致每个分箱内的样本量太少而失去统计意义;分箱数太少,又会导致计算结果精度降低。 - step2: 按相同分箱区间,对实际分布(actual)统计各分箱内的样本占比。
- step3:计 算各分箱内的A - E和Ln(A / E),计算index = (实际占比 - 预期占比)* ln(实际占比 / 预期占比) 。
- step4: 将各分箱的index进行求和,即得到最终的PSI。

图 2 - PSI计算表格
在计算得到PSI指标后,这个数字又代表什么业务含义呢?PSI数值越小,两个分布之间的差异就越小,代表越稳定。

图 3 - PSI数值的业务含义
Part 3. 相对熵(KL散度)的理解
相对熵(relative entropy),又被称为Kullback-Leibler散度(Kullback-Leibler divergence)或信息散度(information divergence),是两个概率分布间差异的非对称性度量。
划重点——KL散度不满足对称性。
我们先不考虑相对熵的计算逻辑,先看它的物理含义是什么?
相对熵可以衡量两个随机分布之间的"距离“。
1)当两个随机分布相同时,它们的相对熵为零;当两个随机分布的差别增大时,它们的相对熵也会增大。
2)注意⚠️:相对熵是一个从信息论角度量化距离的指标,与数学概念上的距离有所差异。数学上的距离需要满足:非负性、对称性、同一性、传递性等;而相对熵不满足对称性。
看到这里,是不是感觉和PSI的概念非常相似?
当两个随机分布完全一样时,PSI = 0;反之,差异越大,PSI越大。
直觉告诉我们相对熵和PSI应该存在着某种隐含的关系,真相正在慢慢浮出水面。
我们再来看相对熵的计算公式。在信息理论中,相对熵等价于两个概率分布的信息熵(Shannon entropy)的差值。
(2)KL(P||Q)=−∑x∈XP(x)log1P(x) ∑x∈XP(x)log1Q(x)=∑x∈XP(x)logP(x)Q(x)
其中,P(x)表示数据的真实分布,而Q(x)表示数据的观察分布。上式可以理解为:
概率分布携带着信息,可以用信息熵来衡量。
若用观察分布Q(x)来描述真实分布P(x),还需要多少额外的信息量?