比如一颗行星绕太阳旋转?不论苹果的故事,是否实际真的发生过,牛顿认为,他的想法是很有前景的,引力可能影响一切事物,包括其他行星和卫星的运行轨道,所以他开始寻找方程,能够准确的描述引力使物体运动的方式,不论是苹果落向地面,还是月球绕地球旋转,牛顿知道,不论这种引力如何产生作用,它的表现可能就会像任何其他物体所受的合力一样,它会等于物体的质量乘以物体的加速度
质量m很容易得到,这不过就是苹果的质量,或月球的质量,找出影响方程中加速度a的因素会有点困难,牛顿首先意识到,是他必须考虑的距离,当物体靠近地球表面,比如树上的苹果,引力会使物体以大约10m/s^2加速度,但月球的加速度只有下落苹果的大约1/3600,月球离地心的距离恰好同样是苹果离地心距离的大约60倍。60的平方就是3600

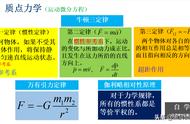
所以牛顿发现,两个物体之间引力一定随距离增大而减小,更确切的说,引力大小一定取决于两个物体距离的平方。

然后是质量,不是苹果或月球的质量,而是参与引力舞蹈中的另一个物体的质量,这个例子中,地球。牛顿意识到,两个相互拉动的物体的质量越大,它们之间的引力就越强,一旦他考虑了两个物体之间的距离,它们的质量,牛顿引力方程的大部分已经完成。
引力与两个物体质量的乘积,除以物体距离的平方,成一定的比例

但引力必须要小的多,否则,你就会看到引力会拉动日常生活中的几乎任何物体,比如,正待在原地不动的书本,而不是被拉向我,所以我和书本之间的引力一定非常小,于是牛顿在它的方程中添加了一个常数,一个非常小的数字,会使引力计算出来比原来的结果小很多,他称之为G